A step by step tutorial, with detailed solutions, on how to find the domain and range of real valued functions is presented. First the definitions of these two concepts are presented. A table of domain and range of basic functions might be useful to answer the questions below.

Definition of the Domain of a Function For a function f defined by an expression with variable x, the implied domain of f is the set of all real numbers variable x can take such that the expression defining the function is real. The domain can also be given explicitly. also Step by Step Calculator to Find Domain of a Function Definition of the Range of a Function The range of f is the set of all values that the function takes when x takes values in the domain. Also a Step by Step Calculator to Find Range of a Function is included in this website. Examples with Detailed Solutions Example 1 Find the domain of function f defined by Solution to Example 1 x can take any real number except 1 since x = 1 would make the denominator equal to zero and the division by zero is not allowed in mathematics. Hence the domain in interval notation is given by the set (- ∞ , 1) U (1 , + ∞) Matched Problem 1 Find the domain of function f defined by Answers to matched problems 1,2,3 and 4 Example 2 Find the domain of function f defined by Solution to Example 2 The expression defining function f contains a square root. The expression under the radical has to satisfy the condition 2x - 8 >= 0    for the function to take real values. Solve the above linear inequality x >= 4 The domain, in interval notation, is given by [4 , +∞) Matched Problem 2 Find the domain of function f defined by: Example 3 Find the domain of function f defined by: Solution to Example 3 The expression defining function f contains a square root. The expression under the radical has to satisfy the condition -x ≥ 0 Which is equivalent to x ≤ 0 The denominator must not be zero, hence x not equal to 3 and x not equal to -5. The domain of f is given  by (-∞ , - 5) ∪ ( - 5 , 0] Matched Problem 3 Find the domain of function f defined by: Example 4 Find the range of function f defined by: Solution to Example 4 The domain of this function is the set of all real numbers. The range is the set of values that f(x) takes as x varies. If x is a real number, x2 is either positive or zero. Hence we can write the following: x 2 ≥ 0 Subtract - 2 to both sides to obtain x 2  - 2 ≥ - 2 The last inequality indicates that x2 - 2 takes all values greater that or equal to - 2. 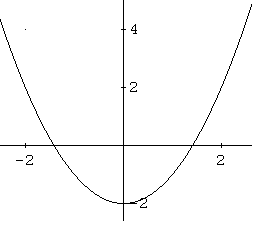The range of f is given by [ -2 , +∞) A graph of f also helps in interpreting the range of a function. Below is shown the graph of function f given above. Note the lowest point in the graph has a y (= f (x) ) value of - 2. Matched Problem 4 Find the range of function f defined by: More Links and References Find domain and range of functions, Find the range of functions, find the domain of a function , Step by Step Solver to Find the Domain of the Square Root of a Linear Function, Find the Domain of the Square Root of a Quadratic Function and mathematics tutorials and problems.