|
Review
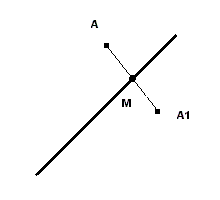
Point A1 is the reflection, across a line, of point A if the midpoint M of points A and A1 is on
the line and segment AA1 is perpendicular to the line of reflection.
Interactive Tutorial Using Java Applet
A - Reflection of a point across a line
1 - click on the button above "click here to start" and MAXIMIZE the window obtained.
2 - Press button "0, 1 or 2 reflections" to obtain one reflection only (red line). compare the distances from A to the line of reflection and from A1 to the same line. Are they equal? How is the angle between segment AA1 and the line of reflection?(If and when dragging a point another point is plotted, delete it using the button "delete last point"). Drag point A and repeat untill you are sure you understand the definition given above.
3 - Drag point A so that it is on the line of reflection, Where is point A1? Explain.
4 - Change the position of the line of reflection using the top scroll bar (red line) and examine the distances as above and the angle between AA1 and the line of reflection.
5 - Click on the button "0, 1 or 2 reflections" in order to have two reflections. After a
reflection across the "red" line, point A1 is reflected a second time across the "purple" line.
Rotate the purple line so that it is in the same position as the red line (same line). Explain
why point A and A2 are in the same position.
B - Reflection of a figure across a line
6 - Click on the button "0, 1 or 2 reflections" in order to have 1 reflection. To generate a
figure such as a triangle, rectangle or an even more complicated figures, click anywhere on the
plot screen to plot connected points and adjust the position of these points by dragging them.
7 - Draw a triangle by clicking at three different positions. Compare the original triangle and
the reflected triangle. Click on the button "0, 1 or 2 reflections" to have two reflections.
Compare now the three triangles. Change the position of one of the two lines of reflection such that the two line are in the same position. Compare the original triangle with the twice (purple) reflected triangle. Explain.
8 - Reset and click on the button "0, 1 or 2 reflections" to have no reflection. Adjust the red line so that it is vertical. Draw a square with vertices at the points
(-1,1), (1,1), (1,3) and (-1,3). The square has one half on the right of the red line and the other half on the left of the same line as shown below.
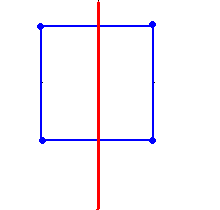
click on the button "0, 1 or 2 reflections" to have 1 reflection. Explain why the square reflects onto itself. Can you think of other figures that have this property? Draw them and see the results.
9 - Reset and click on the button "0, 1 or 2 reflections" to have no reflection. Plot a point and draw on paper where its reflection would be. click on the button "0, 1 or 2 reflections" to have 1 reflection and compare. Repeat for different points with one and two reflections untill you can do this exercise without any difficulties.
10 - Reset and click on the button "0, 1 or 2 reflections" to have no reflection. Draw a triangle. On paper draw where the reflected triangle. click on the button "0, 1 or 2 reflections" to have 1 reflection and compare. Repeat for different triangles with one and two reflection untill you can do this exercise without any difficulties.
11 - Repeat activity 10 with more complicated shapes.
More
Geometry Tutorials, Problems and Interactive Applets.
|

