Problem

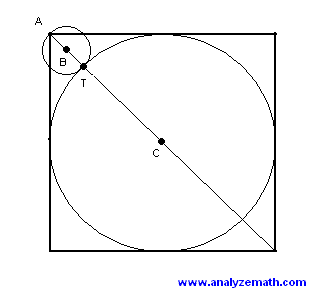
2 Methods to solve the above problem
METHOD 1

• From point T, we draw TM and TN where points M and N are points of intersection of the small circle with the large square. Since AT is a diameter, AMT and ANT are right angles. Because of symmetry, the lengths of the cords AM and AN are equal and therefore AMTN is a square. The diagonal of this small square is equal to the diameter of the small circle. Since we know the perimeter, the diameter d is given by
  
  d = perimeter / π = 4 π / π = 4
  
• Now that we have the diagonal of the small square, we find the length of its sides as follows
  AN² + NT² = 4²
  
• Solve to obtain
  AN = NT = 2sqrt(2)
  
• We now consider the rigth triangle TPC and use Pythagora's theorem to write
  x ² + y ² = r ²
  
• Note that
  x = r - AN = r - 2sqrt(2) and y = r - NT = r - 2sqrt(2)
  
• Substitute x and y in the equation x ² + y ² = r ² and write
  (r - 2sqrt(2)) ² + (r - 2sqrt(2)) ² = r ²
  
• Group like term
  2 (r - 2 sqrt(2)) ² = r ²
  
• Extract the square root to obtain two equations
  sqrt(2) (r - 2sqrt(2)) = r or sqrt(2) (r - 2sqrt(2)) = - r
  
• The above equations gives two solutions but only one is valid and is given by.
  r = 4 + 4sqrt(2)
  METHOD 2
  
• Consider the right triangle AQC and use Pythagora's theorem to write
  r ² + r ² = (r + 4) ²
  
• Expand and solve to obtain 2 solutions to the above equation but again only one of them is valid and is given by r = 4 + 4sqrt(2).

More References and Links to Geometry Problems