Triangle and Tangent Circle - Problem With Solution

A problem, on a triangle tangent at two points to a circle, is presented along with detailed solution.

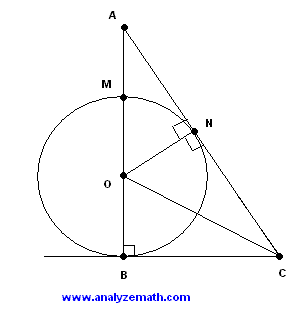
Problems

In the figure below, triangle ABC is tangent to the circle of center O at two points. The lengths of AM and BC are equal to 6 and 18 cm respectively. Find the radius of the circle.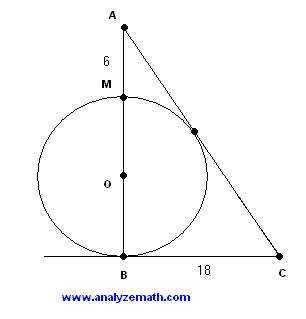
Triangle and Tangent Circle - problem

Solution to Problem :

  • Let B and N be the two points of tangency of the circle (see figure below). We then have three right triangles. We first use Pythagora's theorem to triangle AON. Let r be the length of the radius of the circle. Hence
    Triangle and Tangent Circle - solution

    AN 2 + r 2 = (r + 6) 2
  • Solve the above fo AN
    AN = SQUARE ROOT [ 36 + 12 r]
  • Also triangles ONC and OBC are right triangles such that ON = OB and therefore congruent. Hence NC = BC = 18 cm. Use Pythagora's theorem to triangle ABC
    (6 + 2r) 2 + 18 2 = (18 + AN) 2
  • Expand the above equation and group like terms
    4 r 2 + 12 r = 36 AN
  • Substitute AN by SQUARE ROOT [ 36 + 12 r] and divide all terms by 4
    r 2 + 3 r = 9 SQUARE ROOT [ 36 + 12 r]
  • Square both sides
    ( r 2 + 3 r ) 2 = 9 2 [ 36 + 12 r]
  • Expand and group
    r 4 + 6 r 3 + 9 r 2 - 972 r - 2916 = 0
  • The above equation has two real solutions. Only one of them is positive and is equal to 9 cm.


More References and Links to Geometry Problems

Geometry Tutorials, Problems and Interactive Applets.