where \( r \) is the radius of the circular base and \( h \) is the height of the cone.
Problem 1
Find a formula for the area of the lateral surface of the cone shown on the left above. Solution to Problem 1:
- When cut open along the slant height \( H \) and flattened, the cone becomes a sector of a circle as shown in the figure above right. Therefore, the area of the lateral surface of the cone is equal to the area of the sector shown on the right. The length \( S \) of the arc of the sector is the perimeter of the base of the cone and is given by: \[ S = 2 \pi r \]
- Also, the relationship between \( S \), the central angle \( \theta \), and \( H \) the radius of the sector is: \[ S = \theta H \]
- Equating the right sides of \( S = 2 \pi r \) and \( S = \theta H \), and solve for \( \theta \) to obtain: \[ \theta = \frac{2 \pi r}{H} \]
- The area \( A \) of the sector is given by: \[ A = \frac{1}{2} \theta H^2 = \frac{1}{2} \left( \frac{2 \pi r}{H} \right) H^2 \]
- Simplify to obtain the area of the sector, which is also the lateral surface of the cone: \[ A = \pi r H \]
- We now return to the cone and consider triangle \( OCM \), which is a right triangle. Using Pythagoras' theorem: \[ H = \sqrt{h^2 + r^2} \]
- Substitute the above expression for \( H \) into the formula for \( A \) to obtain an expression in terms of \( r \), the radius of the base, and \( h \), the height of the cone. \[ A = \pi r \sqrt{h^2 + r^2} \]
Problem 2
A tool is made up of a cone on top of a cylinder (see figure below). The cylinder has a height \( h \) of 15 cm and a radius of 5 cm. The volume of the cone is \( 100 \pi \) cm\(^3\). \( O \) is the vertex of the cone, \( AB \) is the diameter of the base of the cone, and \( C \) its center. Points \( O \), \( A \), \( B \), and \( C \) are in the same plane.1 - Approximate angle \( \angle AOB \).
2 - Calculate the area of the lateral surface of the tool.
Solution to Problem 2:
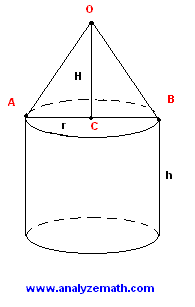
- Note that the radius of the cylinder and the radius of the base of the cone have the same size. We first use the formula for the volume of the cone to find its height \( H \): \[ \frac{1}{3} \pi 5^2 H = 100 \pi \]
- Solve for \( H \): \[ H = 12 \, \text{cm} \]
- Since \( OC \) is orthogonal to the base, triangle \( AOC \) is a right triangle. The tangent of angle \( AOC \) is given by: \[ \tan(\angle AOC) = \frac{r}{H} = \frac{5}{12} \] \[ \angle AOC = \arctan \left( \frac{5}{12} \right) \]
- Because of the symmetry of the tool, the size of angle \( AOB \) is twice the size of angle \( AOC \), hence: \[ \angle AOB = 2 \arctan \left( \frac{5}{12} \right) = 45.2^\circ \quad \text{(approximated to 1 decimal place).} \]
- The area of the lateral surface of the cone and that of the cylinder are added to obtain the total area \( A \) of the surface: \[ A = \pi r \sqrt{H^2 + r^2} + 2 \pi r h \] \[ A = \pi \cdot 5 \cdot \sqrt{12^2 + 5^2} + 2 \pi \cdot 5 \cdot 15 \] \[ A = 675.4 \, \text{cm}^2 \quad (\text{approximated to 1 decimal place}). \]
More References and Links to Geometry
- Surface Area and Volume of Right Cone Calculator. An easy to use online calculator to calculate the lateral surface area and the volume of a right cone given its radius and height.
- Make a Cone from a Sector Calculator. An easy to use online calculator to calculate the central angle and radius of sector to make a cone.
- Geometry Tutorials, Problems and Interactive Applets.