If you cut off the top part of a cone with a plane perpendicular to the height of the cone, you obtain a conical frustum. See figure on the left: the upper base of the frustum has radius r and the lower base has radius R. The height of the frustum is h.
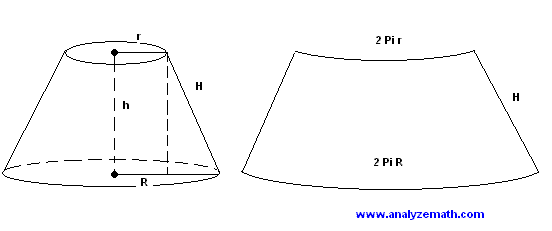
On the right is the shape obtained if the frustum on the left is cut along the slanted height H. This shape may be used to construct a conical frustum. It is part of a sector of a circle; see figure below. Let us start by expressing H in terms of r, R and h. We use Pythagora's theorem in the right triangle on the left whose hypotenuse is H, as follows:
H 2 = h 2 + (R - r) 2
hence
H = sqrt [ h 2 + (R - r) 2 ]
If you now prolong the sides of the figure on the right above, you obtain the sector shown below.
To construct the frustum, you need to find x, y and the central angle t. Using the arc length formula, we can write:
2 Pi r = x t
and
2 Pi R = y t
The above formulas may be used to write:
2 Pi R / 2 Pi r = y t / x t
which can be simplified to give:
R / r = y / x
We can also write:
y = x + H
Substitute y = x + H in R / r = y / x and solve for x:
R / r = (x + H) / x
R x = r x + r H
R x - r x = r H
x = r H / (R - r)
We now use y = x + H to find y:
y = r H / (R - r) + H
Any of the formula 2 Pi r = x t or 2 Pi R = y t may be used to find the central angle t (in radians):
t = 2 Pi r / x
= 2 Pi r / [ r H / (R - r) ]
= 2 Pi (R - r) / H
Example
Find H, x, y and t for a frustum with r = 10 cm, R = 20 cm and h = 25 cm.First find H.
H 2 = 25 2 + (20 - 10) 2
H = sqrt (725) cm
x = r H / (R - r)
= 10 sqrt (725) / (20 - 10) = sqrt (725) cm
y = x + H = 2 sqrt (725) cm
t = 2 Pi r / x
= 2 Pi 10 / sqrt (725)
In degrees, angle t is given by
t = 180 [ 2 Pi 10 / sqrt (725) ] / Pi
= 133.7 degrees (rounded to 1 decimal place).
Surface Area and Volume of Frustum - Geometry Calculator. Calculate the surface area, the volume and other parameters of a Frustrum given its radius R at the base, its radius r at the top and its height h.
