Triangle Inscribed in a Circle - Problem With Solution

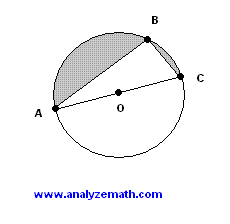Solution to Problem :

• If the center O is on AC then AC is a diameter of the circle and the triangle has a right angle at B (Thales's theorem). If At is the area of triangle ABC and As the shaded area then
  
  
  
  At = 2 As
  
  
• We also have.
  
  At + As = (1/2) area of circle = (1/2) Pi 10 ² = 50 Pi
  
  2 As + As = 50 Pi
  
  
• Which gives.
  
  As = 50 Pi / 3
  
  
• Since triangle ABC has a right angle, we now use the internal angle (to the triangle) A to write.
  
  sin(A) = CB / AC = CB / 20 which gives CB = 20 sin (A)
  
  and cos(A) = AB / AC = AB / 20 which gives AB = 20 cos (A)
  
  
• The area As might also be written as follows (using the identity sin(2A) = 2 sin (A) cos (A)).
  
  As = (1/2) * AB * CB = 200 cos (A) sin(A) = 100 sin (2A) = 50 Pi / 3
  
  
• The above equation gives.
  
  sin (2A) = 0.5 Pi / 3
  
  
• Use calculator to solve for 2A. Two solutions
  
  2A = 31.6 degrees (nearest tenth) or A = 15.8 degrees
  
  2A = 148.4 degrees (nearest tenth) or A = 74.2 degrees
  
  
• We now calculate the lengths of AB and CB. Two solutions
  
  first solution
  
  AB = 20 cos (15.8) = 19.24 (2 decimals) and CB = 20 sin (15.8) = 5.45 (2 decimals)
  
  second solution
  
  AB = 20 cos (74.2) = 5.45 (2 decimals) and CB = 20 sin (74.2) = 19.24 (2 decimals)
  
  
• The two solutions correspond to two congruent right triangles.

More references to geometry problems.