Area Of Octagon - Problem With Solution

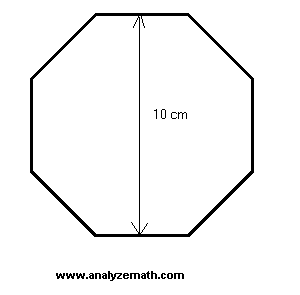
Solution to the Problem:

• The octagon has 8 interior angles. The measure of one interior angle ABD is given by
  (8 - 2)*180 / 8 = 135 degrees
  

  
  
  

• Draw AC and BC so that they are perpendicular at C. Hence the measure of ABC is given by
  135 - 90 = 45degrees
  
  
• Note that triangle ABC is right and isosceles. We now write that the given distance of 10 cm is the sum of 2y and x
  
  2y + x = 10
  
  
• Using Pythagora's theorem, we can also write
  
  2y² = x²
  
  
• We now solve the above system of equations to obtain x, the length of one side.
  
  x = 10 / (1 + sqrt(2)) cm
  
  
• The perimeter P is given by.
  
  P = 8*10 / (1 + sqrt(2)) = 80 / (1 + sqrt(2)) cm
  
  
• The area A may be calculated by subtracting the areas of the 4 right triangles from the area of the large square of side 10 cm.
  
  A = 10*10 - 4(1/2)(y²) = 100 - 2(y²) = 100 - (x²) = 200(sqrt(2)-1) cm²

More references on geometry.