Parallelogram Problems

Word problems on parallelogram with detailed solutions are presented.

Formula for Area of Parallelogram

Area = b × h , b is the base and h is altitude.

Problem 1

Show that the quadrilateral ABCD, where the vertices are defined by their coordinates as follows: A(-2, 0), B(2 , 4), C(4 , 1) and D(0 , -3), is a parallelogram.

Solution to Problem 1:

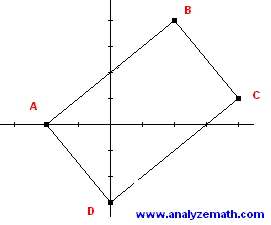
    parallelogram used in solution of problem 1
  • To show that the given quadrilateral is a parallelogram we need to show that it has two pairs of parallel and congruent sides. So we need to find the slopes and the lengths of all segments making the quadrilateral.
    slope of AB = (4 - 0) / (2 - (-2)) = 1
    slope of BC = (1 - 4) / (4 - 2) = - 3 / 2
    slope of CD = (-3 - 1) / (0 - 4) = 1
    slope of AB = (-3 - 0) / (0 - (-2)) = - 3 / 2
    distance of AB = sqrt (4 2 + 4 2) = 4 sqrt (2)
    distance of BC = sqrt (2 2 + (-3) 2) = sqrt (13)
    distance of CD = sqrt (4 2 + 4 2) = 4 sqrt (2)
    distance of DA = sqrt ((-2) 2 + 3 2) = sqrt (13)
  • Segments AB and CD have equal slopes and are therefore parallel. Their lengths are also equal. Segments BC and DA have equal slopes and are therefore parallel. They also have equal lengths. These are the properties of a parallelogram.

Problem 2

Given the length (in feet) of side AB and the internal angle D of the parallelogram below, find its height h and the length of side BC given that the area of the parallelogram is equal to 1000 feet 2.
parallelogram used in problem 2

Solution to Problem 2:

  • Since it is a parallelogram internal angles A and D are supplementary and their sum is equal to 180 degrees. Hence the size of angle A is given by
    A = 180 - 135 = 45 degrees.
  • We now use the right triangle ABB' to find the height h.
    sin 45o = h / 15
  • with sin 45o = sqrt (2) / 2, we obtain
    h = 15 sqrt (2) / 2
  • The area of a parallelogram is given by
    Area = length of BC * h
  • Substitute the area and the height h by their values in the above equation and solve for BC
    length of BC = 1000 / [ 15 sqrt (2) / 2] = 94.28 feet
    (rounded to two decimal places).

Problem 3

In the parallelogram below, BB' is the angle bisector of angle B and CC' is the angle bisector of angle C. Find the lengths x and y if the length of BC is equal to 10 meters.
parallelogram used in problem 3

Solution to Problem 3:

  • Note that the internal angles B and C are supplementary angles and their sum is equal to 180 degrees. Note also that the size of angle BCO is half the size of internal angle C; and the size of angle CBO is half the size of the internal angle B. Hence
    size of angle BCO + size of angle CBO = 1/2 size of angle C + 1/2 size of angle B = 90 o
  • Since the sum af all angles in a triangle is equal to 180 degrees, angle BOC is a right angle and the triangle BOC is a right triangle. Also angle angles A and C are equal hence angle BCO is equal to 30 degrees. The lengths x and y may be calculated using the trigonometric ratios as follows.
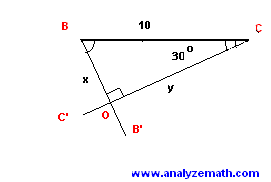
    triangle used in solution of problem 3

  • sin 30o = x / 10
    x = 10 * sin 30o = 5 meters.
    cos 30o = y / 10
    y = 10 * cos 30o = 5 sqrt (3) meters.

Problem 4

The parallelogram shown below has an area of 300 squared feet. Find all its internal angles.
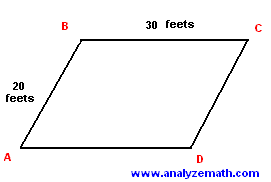parallelogram used in problem 4

Solution to Problem 4:

  • The area of the parallelogram may be calculated as the sum of the area of the two congruent triangles ABC and ACD. The area of triangle ABC is given by:
    area of ABC = (1 / 2) sin (B) * 30 * 20
  • The total area of the parallelogram is twice the area of triangle ABC.
    area of ABCD = 2 * (1 / 2) sin (B) * 30 * 20 = 300
  • Solve the above for sin (B) to obtain.
    sin (B) = 1 / 2
    size of angle B = (180 - 30) degrees = 150 degrees.
    size of angle C = 180 - 150 = 30 degrees , B and C are supplementary angles.
    size of angle D = size of angle B = 150 degrees.
    size of angle A = size of angle C = 30 degrees.

More References and Links to Geometry Problems

Geometry Tutorials, Problems and Interactive Applets.