Rectangle Problems

Rectangle problems with detailed solutions.

Perimeter of a Rectangle


  • Perimeter = 2 W + 2 L , w is the width and L is the length of the rectangle.

    Area of a Rectangle


    • Area = L × W , w is the width and L is the length of the rectangle.

    Problems with Solutions


    Problem 1

    A rectangle has a perimeter of 320 meters and its length L is 3 times its width W. Find the dimensions W and L, and the area of the rectangle.

    Solution to Problem 1:

    • Use the formula of the perimeter to write.
      2 L + 2 W = 320
    • We now rewrite the statement "its length L is 3 times its width W" into a mathematical equation as follows:
      L = 3 W
    • We substitute L in the equation 2 L + 2 W = 320 by 3 W.
      2(3 W) + 2 W = 320
    • Expand and group like terms.
      8 W = 320
    • Solve for W.
      W = 40 meters
    • Use the equation L = 3 W to find L.
      L = 3 W = 120 meters
    • Use the formula of the area.
      Area = L W = 120 * 40 = 4800 meters 2

    Problem 2

    The perimeter of a rectangle is 50 feet and its area is 150 feet 2. Find the length L and the width W of the rectangle, such that L > W.

    Solution to Problem 2:

    • Use the formula of the perimeter to write
      2 L + 2 W = 50
    • and the formula of the area to write
      L W = 150
    • Divide all terms in the equation 2 L + 2 W = 50 by 2 to obtain
      L + W = 25
    • Solve the above for W
      W = 25 - L
    • Substitute W by 25 - L in the equation L W = 150
      L(25 - L) = 150
    • Expand the above equation and rewrite with right term equal to zero.
      -L 2 + 25 L - 150 = 0
    • The above is a quadratic equations with two solutions.
      L = 10 and L = 15
    • Use W = 25 - L to find the corresponding values of W.
      W = 15 and W = 10
    • Since L > W, the rectangle has the dimensions
      L = 15 feet and W = 10 feet.
    • As an exercise, check that the area and perimeter of the rectangle are 150 and 50 respectively.

    Problem 3

    The diagonal d of a rectangle has a length of 100 feet and its length y is twice its width x (see figure below). Find its area.
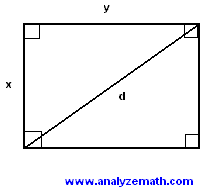    rectangle problem 3

    Solution to Problem 3:

    • We first use Pythagora's theorem.
      100 2 = x 2 + y 2
    • We rewrite the statement "its length y is twice its width x" as a mathematical equation.
      y = 2 x
    • Substitute y by 2 x in the equation 100 2 = x 2 + y 2.
      100 2 = x 2 + (2 x) 2
    • Expand and group like terms.
      100 2 = 5 x 2
    • Solve for x, with x positive.
      x = 20 sqrt(5) feet
      and
      y = 40 sqrt(5) feet.
    • Area is given by
      Area = y x = 40 sqrt(5) * 20 sqrt(5) = 4000 feet 2.

    Problem 4

    Are the points A(-1 , 0), B(5 , 2), C(4 , 5) and D(-2 , 3) the vertices of a rectangle?
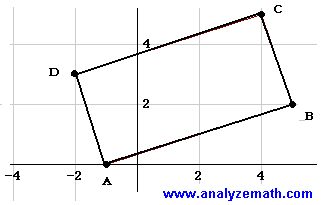    rectangle problem 4

    Solution to Problem 4:

    • We first calculate the slopes and see if the opposite sides are parallel.
      mAB = (2 - 0) / (5 - (-1)) = 1 / 3
      mBC = (5 - 2) / (4 - 5) = -3
      mCD = (3 - 5) / (-2 - 4) = 1 / 3
      mDA = (0 - 3) / (-1 - (-2)) = -3
    • Note that the slope of sides AB and CD are equal to 1 / 3 and therefore these two sides are parallel. Also the slopes of BC and DA are equal and therefore these two sides are parallel. ABCD is a parallelogram. Also the product of the slopes of AB and BC is equal to -1 and therefore AB is perpendicular to BC. Therefore the quadrilateral ABCD is a rectangle.

    More References and Links to Geometry

    Geometry Tutorials, Problems and Interactive Applets.
     

    Social

    Navigation

    Search