Geometry Problems on Squares
Problems on area and perimeter of squares with detailed solutions are presented.
Area and Perimeter of a SquarePerimeter of a Square
Perimeter = 4 S , S is the side length of the square.
Area of a Square
Area = S 2 , S is the side length of the square.
Problems with Deatiled SolutionsProblem 1
When the sides of a square are each increased by 2 feet its area increases by 44 feet 2. Find the side length S before the increase.
Solution to Problem 1:
-
Let S be the side length before the increase, the area A1 is given by
A1 = S 2
-
Let S + 2 the side after the increase, the area A2 is given by
A2 = (S + 2) 2
-
But A2 = A1 + 44, hence
A1 + 44 = (S + 2) 2
-
Substitute A1 by S 2
in the above equation.
S 2 + 44 = (S + 2) 2
-
Expand, group like terms and rewrite the equation as follows.
4 S = 40
-
Solve for S.
S = 10 feet.
-
As an exercise, find areas for S = 10 and for S = 12 and check the the difference is 44 feet 2.
Problem 2
Find the area and perimeter of a square with diagonal of 200 meters.
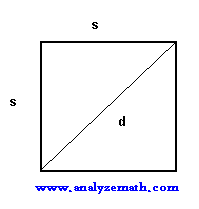 Solution to Problem 2: Solution to Problem 2:
-
Use Pythagora's theorem to write
S 2 + S 2 = 200 2
-
Solve for S 2 to find the area
S 2 = 20000 m 2
-
We need to find S to find the perimeter
S = 100 sqrt(2)
Perimeter = 4 S = 400 sqrt(2) m.
Problem 3
What happens to the area of a square if we double its side?
Solution to Problem 3:
-
The area A1 of a square of side length S is given by.
A1 = S 2
-
Double the side to 2S and find the new area A2.
A2 = (2 S) 2 = 4 S 2
-
The area is multiplied by 4.
Problem 4
A square garden (green) of 400 m 2 is to be surrouned by a walkway (yellow) of constant width x. The total area of the walkway has to be 500 m 2. Find the width x of the walkway.
 Solution to Problem 4: Solution to Problem 4:
-
The total area A of the garden and the walkway is given by.
A = 400 + 500 = 900 m 2
-
The side S of the garden is given by.
S = sqrt(400) = 20 m
-
The outside of the walkway is a square of side
S + x + x = S + 2x = 20 + 2x.
-
The total area of the large square is equal to 900 m 2, hence the equation:
(20 + 2x) 2 = 900
-
We now solve for x
x = 5 and x = -25
-
x is a measure of length and has to be positive, hence
x = 5 meters.
-
As an exercise, find the side of the larger square and its area and check with the total value of the area 900 m. 2
More References and Links to Geometry ProblemsGeometry Tutorials, Problems and Interactive Applets.
|


