Trapezoid Problems
Trapezoid problems are presented along with their with detailed solutions.
Area of Trapezoid Formula
Area = 0.5 h (a + b)
where h is the altitude of the trapezoid and a and b are the lengths of the bases.
Problem 1
A trapezoid ABCD with AD parallel to BC has angle D equal to 40 degrees, the length of DC is equal to 2 meters, the length of BC is equal to 5 meters and the area of the trapezoid is equal to 20 m 2. Calculate the length of AD. (dimensions in figure below are not accurate).
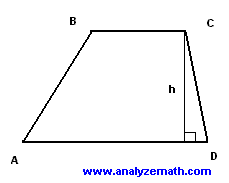Solution to Problem 1:
- Use the sine definition in a right triangle to find the height h of the trapezoid.
sin D = h / CD
- Solve the above for h.
h = CD sin D = 2 sin 40
- Use the formula of the area to obtain the following equation.
area of trapezoid ABCD = 0.5 * h * (BC + AD)
- The above equation has only one unknown: AD. Substitute all the known quantities to obtain
20 = 0.5 * 2 * sin 40 *(5 + AD)
- Solve for AD.
AD = 20 / (0.5*2*SIN 40) - 5 = 26.11 meters (approximated to two decimal places).
Problem 2
Show that the quadrilateral ABCD whose vertices are defined by their coordinates as follows A(-2,0), B(2,4) , C(2,1) and D(1,0) is a trapezoid and find its area.
Solution to Problem 2:
- If we can show that two sides are parallel then the quadrilateral defined above is a trapezoid. Since we are given the coordinates of these points, we calculate the slopes of these segments and check if they are parallel.
slope of AB = (4 - 0) / (2 - -2) = 1
slope of BC = (1 - 4) / (2 - 2) = undefined slope , BC vertical.
slope of CD = (0 - 1) / (1 - 2) = 1
slope of DA = (0 - 0) / (-2 - 1) = 0 , DA horizontal.
- The values of the slopes above show that AB and CD area parallel (slope equal to 1) while BC and DA are not parallel and therefore the given quadrilateral is a trapezoid. See figure below
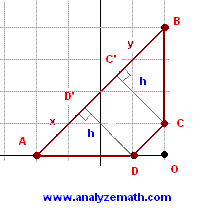
- One way to calculate the area is to subtract the area of the right triangle ODC from the area of the large right triangle OAB.
Area of triangle ODC = 0.5 * OD * OC = 0.5 * 1 * 1 = 0.5
Area of triangle OAB = 0.5 * OA * OB = 0.5 * 4 * 4 = 8
Area of Trapezoid ABCD = 8 - 0.5 = 7.5 unit 2
Problem 3
Find the area of the trapezoid ABCD given the length of its 4 sides.
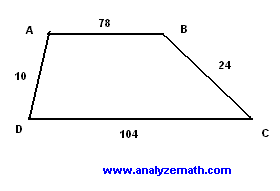Solution to Problem 3:
- We first prolong sides DA and CB of the trapezoid so that they intersect at point O.(see figure below). The area of the trapezoid may be found by subtracting the area of the triangle AOB from the area of triangle DOC.
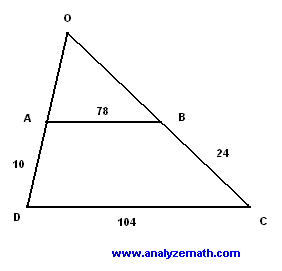
- ABCD is a trapezoid and the its bases AB and DC are parallel. Since AB and DC are parallel the triangles AOB and DOC are similar hence the proportinality of the corresponding sides.
OA / OD = OB / OC = AB / DC = 78 / 104 = 3 / 4
- Use equation OA / OD = 3 / 4 and solve for OA.
OA / (OA + 10) = 3 / 4
OA = 30
- Use equation OB / OC = 3 / 4 and solve for OA.
OB / (OB + 24) = 3 / 4
OB = 72
- We now use Heron's formula to find area of triangle AOB.
S = 0.5 * (AO + OB + BA) = 0.5 * (30 + 72 + 78) = 90
area = sqrt [ s(s - AO)(S - OB)(S - BA) ] = sqrt [ 90(90 - 30)(90 - 72)(90 - 78) ] = 1080 unit 2
- We now use Heron's formula again to find area of triangle DOC.
S = 0.5 * (DO + OC + CD) = 0.5 * (40 + 96 + 104) = 120
area = sqrt [ s(s - DO)(S - OC)(S - CD) ]
= sqrt [ 120(120 - 40)(120 - 96)(120 - 104) ] = 1920 unit 2
- The area of the trapezoid is given by
1920 - 1080 = 840 unit 2
More References and Links to Geometry Problems
Geometry Tutorials, Problems and Interactive Applets.
Trapezoid Area Calculator. Calculator to calculate the area of a trapezoid given the bases and the height.
Trapezoid Calculator and Solver. An easy to use online calculator to solve trapezoid problems. The area, the angles and the diagonals of a Trapezoid are calculated given its 4 sides.