Solve a Trapezoid Given its Bases and Legs

A trapezoid with bases b and d (d > b), legs a and c, and AD and BC are parallel is shown below . Calculate all its angles and its height h.

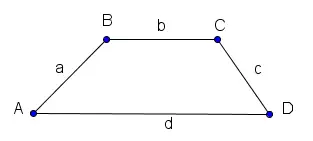
Angles of a Trapezoid Using the trapezoid above, we draw BB' parallel to CD. Using the triangle ABB', we use the cosine rule to write c2 = a2 + (d-b)2 - 2 a (d - b) cos(?BAD) cos(?BAD) = (a2 + (d-b)2 - c2) / (2 a (d - b) ) ?BAD = arccos ( (a2 + (d-b)2 - c2) / (2 a (d - b) ) ) In the same figure, ?BB'A and ?CDA have the same size. Using the same triangle, we use the cosine rule again to write a2 = c2 + (d-b)2 - 2 c (d - b) cos(?BB'A) cos(?BB'A) = (c2 + (d-b)2 - a2) / (2 c (d - b) ) ?CDA = ?BB'A = arccos ( (c2 + (d-b)2 - a2) / (2 c (d - b) ) ) In the given trapezoid, AD and BC are parallel. Hence the pairs of angles BAD and ABC and CDA and DCB are supplementary. 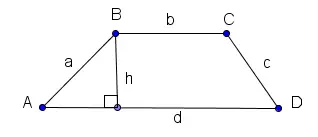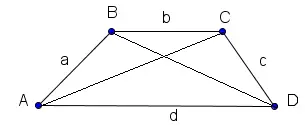Hence ABC = 180° - BAD and DCB = 180° - CDA Height and Area of a Trapezoid h = a cos (?BAD) area = (1/2)(b + d) h Diagonals of a Trapezoid Use cosine rule in triangles DAB and BCD to write: BD2 = a2 + d2 - 2 a d cos (? BAD) BD = √ (a2 + d2 - 2 a d cos (? BAD)) CA2 = c2 + d2 - 2 c d cos (? CDA) CA = √ (c2 + d2 - 2 c d cos (? CDA)) More References and Links to Geometry Geometry Tutorials, Problems and Interactive Applets. Trapezoid Area Calculator. Calculator to calculate the area of a trapezoid given the bases and the height. Trapezoid Calculator and Solver. An easy to use online calculator to solve trapezoid problems. The area, the angles and the diagonals of a Trapezoid are calculated given its 4 sides.