Slope of a Line

Definition of Slope

The slope of a line measures its steepness and rate of change. Given two points \(A(x_A,y_A)\) and \(B(x_B,y_B)\), the slope \(m\) is defined as:

\[ m = \frac{\Delta y}{\Delta x} = \frac{y_B - y_A}{x_B - x_A} \]

Where \(\Delta y = y_B - y_A\) is the vertical change (rise) and \(\Delta x = x_B - x_A\) is the horizontal change (run).

Special Cases

Horizontal Lines

For horizontal lines, \(y_A = y_B\), so:

\[ m = \frac{0}{x_B - x_A} = 0 \]

The equation of a horizontal line is \(y = \text{constant}\).

Vertical Lines

For vertical lines, \(x_A = x_B\), so:

\[ m = \frac{y_B - y_A}{0} = \text{undefined} \]

The equation of a vertical line is \(x = \text{constant}\).

Example Problems

Example 1: Finding Slopes

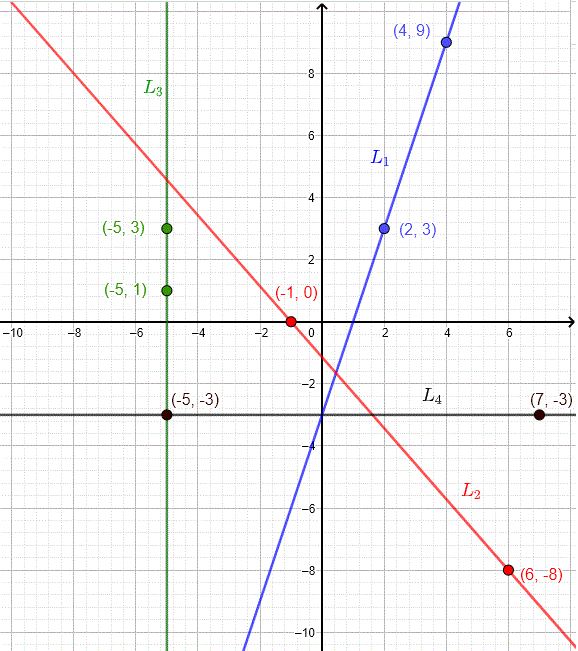
Determine slopes of lines through given points:

\(L_1: (2,3), (4,9) \quad m_1 = \frac{9-3}{4-2} = 3\) (rises)
\(L_2: (-1,0), (6,-8) \quad m_2 = \frac{-8-0}{6-(-1)} = -\frac{8}{7}\) (falls)
\(L_3: (-5,1), (-5,3) \quad m_3 = \frac{3-1}{-5-(-5)} = \text{undefined}\) (vertical)
\(L_4: (7,-3), (-5,-3) \quad m_4 = \frac{-3-(-3)}{-5-7} = 0\) (horizontal)

Example 2: Parallel and Perpendicular Lines

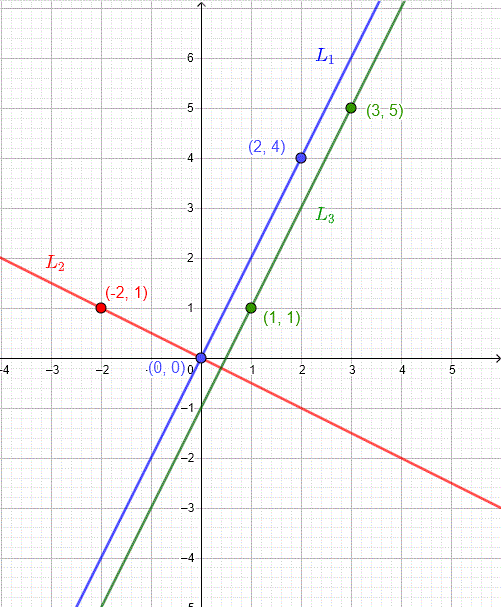
Given lines:

\(L_1: (0,0), (2,4) \quad m_1 = 2\)
\(L_2: (0,0), (-2,1) \quad m_2 = -\frac{1}{2}\)
\(L_3: (1,1), (3,5) \quad m_3 = 2\)

Since \(m_1 = m_3\), \(L_1\) and \(L_3\) are parallel. Since \(m_1 \times m_2 = -1\), \(L_1\) and \(L_2\) are perpendicular.

Interactive Slope Explorer

How to Use the Interactive Graph:

Drag points A and B to change the line's slope
Watch the slope calculation update in real-time
See the rise/run triangle and line equation
Or enter coordinates below and click "Update from Coordinates"

Coordinate Input (Alternative to Dragging)

Point A (Blue)

x_A:

y_A:

Point B (Blue)

x_B:

y_B:

Tip: Drag the blue points on the graph for interactive control!

Slope Calculation

Formula: \(m = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{\text{Rise}}{\text{Run}}\)

Slope (m): 0.833 = 5/6

Equation of line: y = 5/6x - 1.333

\[y = \frac{5}{6}x - 1.333\]

Exploration Activities

Drag point A or B to create different slopes
Make a horizontal line by dragging points to have the same y-coordinate (\(y_A = y_B\))
Make a vertical line by dragging points to have the same x-coordinate (\(x_A = x_B\))
Create positive slopes (line rises left to right)
Create negative slopes (line falls left to right)
Observe how the rise/run triangle changes
Note that slope = rise/run = (\(y_B - y_A\))/(\(x_B - x_A\))