Tangent Function tan x

Definition and Graph of the Tangent Function

We first consider angle \( \theta \) with initial side on the positive x axis (in standard position) and terminal side OM as shown below.
angle in standard position.
The tangent function is defined as \[ \tan(\theta) = \dfrac{y}{x} \] From the definiton of the tangent, we can use the definitions of the \( \sin(\theta) \) and \( \cos(\theta) \) to deduce a relationship between tan, sin and cos functions as follows: \[ \tan(\theta) = \dfrac{y}{x} = \dfrac{y/r}{x/r} = \dfrac{\sin(\theta)}{\cos(\theta)}\] Note that
1) \( \tan(\theta+\pi) = \dfrac{\sin(\theta+\pi)}{\cos(\theta+\pi)} = \dfrac{-\sin(\theta)}{-\cos(\theta)}= \dfrac{\sin(\theta)}{\cos(\theta)} = \tan(\theta)\)
and therefore \( \tan(\theta) \) is a periodic function whose period is equal to \( \pi \).
2) \( \tan(-\theta) = \dfrac{\sin(-\theta)}{\cos(-\theta)} = \dfrac{-\sin(\theta)}{\cos(\theta)} = - \dfrac{\sin(\theta)}{\cos(\theta)} = - \tan(\theta)\)
and therefore \( \tan(\theta) \) is an odd function and its graph is symmetric with respect to the origin of a rectangular system of coordinates.
We now use a unit circle to find \( \sin(\theta)\) and \( \cos(\theta)\) and hence \( \tan(\theta)\) over one period extending from \( \theta = -\dfrac{\pi}{2} \) to \( \theta = +\dfrac{\pi}{2} \).
We know from the sine and cosine functions that the x and y coordinates on a unit circle gives the values of \( \sin(\theta)\) and \( \cos(\theta)\) as shown below.
unit circle to help graph tangent.
Let us now put the values of the angles \( -\dfrac{\pi}{2}, -\dfrac{\pi}{4} , 0 , \dfrac{\pi}{4} , \dfrac{\pi}{2} \) and the values of \cos(\theta) and \sin(\theta) on a table as shown below.

\( \theta \) \( \cos(\theta) \) \( \sin(\theta) \) \( \tan(\theta) = \dfrac{\sin(\theta)}{\cos(\theta)}\)
\( -\dfrac{\pi}{2} \) \( 0 \) \( -1 \) \( undefined \)
\( -\dfrac{\pi}{4} \) \( \dfrac{\sqrt 2}{2} \) \( -\dfrac{\sqrt 2}{2} \) \( -1 \)
\( 0 \) \( 1 \) \( 0 \) \( 0 \)
\( \dfrac{\pi}{4} \) \( \dfrac{\sqrt 2}{2} \) \( \dfrac{\sqrt 2}{2} \) \( 1 \)
\( \dfrac{\pi}{2} \) \( 0 \) \( 1 \) \( undefined \)

\( \tan(\theta)\) is undefined at \( \theta = \dfrac{\pi}{2} \) and \( \theta = - \dfrac{\pi}{2} \), however we can get information about the behaviour \( \tan(\theta)\) close to these values
We use the calculator to find values of \( \tan(\theta)\) as \( \theta \) approaches \( \dfrac{\pi}{2} \approx 1.570796327 \) starting at \( \theta = 1.500000 \)
\( \theta \) \( \tan(\theta) \)
\( 1.500000 \) \( 14.10141995\)
\( 1.550000 \) \( 48.07848248 \)
\( 1.570000 \) \( 1255.765592 \)
\( 1.570700 \) \( 10381.32742 \)
\( 1.570791 \) \( 187730.1491 \)
\( 1.570796 \) \( 3060023.307 \)

As \( \theta \) approaches \( \dfrac{\pi}{2} \) by values smaller than \( \dfrac{\pi}{2} \), \( \tan(\theta) \) approaches large values and hence the existence of a vertical asymptote at \( \theta = \dfrac{\pi}{2} \)
Similarly, as \( \theta \) approaches \( - \dfrac{\pi}{2} \) by values larger than \( - \dfrac{\pi}{2} \) , \( \tan(\theta) \) approaches small values and hence the existence of a vertical asymptote at \( \theta = - \dfrac{\pi}{2} \).
\( \theta \) \( \tan(\theta) \)
\( - 1.500000 \) \( - 14.10141995\)
\( - 1.550000 \) \( - 48.07848248 \)
\( - 1.570000 \) \( - 1255.765592 \)
\( - 1.570700 \) \( - 10381.32742 \)
\( - 1.570791 \) \( - 187730.1491 \)
\( - 1.570796 \) \( - 3060023.307 \)

Using the concept of limits, we describe the behaviour of \( \tan(\theta) \) as \( \theta \) approaches \( \dfrac{\pi}{2} \) from the left (or by values smaller than \( \dfrac{\pi}{2} \)) as follows
\( \lim_{\theta \to (\dfrac{\pi}{2})^-} \tan(\theta) = +\infty \)
and the behaviour of \( \tan(\theta) \) as \( \theta \) approaches \( - \dfrac{\pi}{2} \) from the right (or by values larger than \( - \dfrac{\pi}{2} \)) as follows
\( \lim_{\theta \to (-\dfrac{\pi}{2})^+} \tan(\theta) = -\infty \)
We now use a system of rectangular axes \( (x,y) \) to plot the points in the above table and approximate the graph of the tangent tan x function as shown below.
NOTE
Because we are used to \( x \) being the variable of a function, \(x\) on the graph takes values of \( \theta \) and y takes the values of \( \tan(\theta) \) which is noted as \( y = \tan(x) \).

graph of tan(x) in a rectangular system of axes.

Properties of tan x

1) tan x has a period equal to \( \pi \).
2) \( \tan(x) \) has vertical asymptotes at all values of \( x = \dfrac{\pi}{2} + n\pi \) , \( n \) being any integer.
3) The domain of \( \tan(x) \) is the set of all real numbers except \( x = \dfrac{\pi}{2} + n\pi \) , \( n \) being any integer.
4) The graph of \( \tan(x) \) is symmetric with respect to the origin of the system of axes.
5) The range of \( \tan(x) \) is given by: \( (-\infty , +\infty) \)
6) \( \tan(x) \) is odd and its graph is symmetric with respect to the origin of the system of axes.
7) \( \tan(x) \) is increasing on intervals.

General Tangent Function

The tangent function

\( f(x) = a \tan(b x + c) + d \)

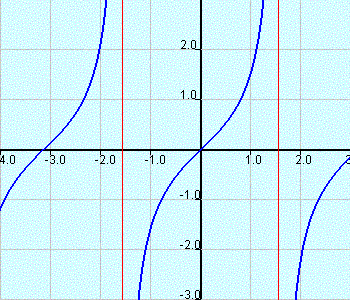
and its properties such as graph, period, phase shift and asymptotes are explored interactively by changing the parameters a, b, c and d using an app. See figure below for main panel of the applet showing the graph of tangent function in blue and the vertical asymptotes in red.
Period of \( f(x) \) is equal to \( \dfrac{\pi}{|b|} \)
Phase Shift of \( f(x) \) is equal to \( - \dfrac{c}{b} \)
tangent function and asymptotes

You may also want to consider another tutorial on the trigonometric unit circle .
Once you finish the present tutorial, you may want to go through a self test on trigonometric graphs .

Interactive Tutorial on Tangent Function


a =
b =
c =
d =
>

How do the 4 coefficients a, b, c and d affect the graph of f(x)?

  1. Set a = 1, b = 1, c = 0 and d = 0. Write down f(x) and take note of the period phase shift and positions of asymptotes (in red) of f(x)? Now change a , how does it affect the graph?
  2. set a = 1, c = 0, d = 0 and change b. Find the period from the graph and compare it to \( pi/|b| \). How does b affect the graph of f(x)? How does it affect the asymptotes?
  3. set a = 1, b = 1, d = 0 and change c starting from zero going slowly to positive large values. Take note of the shift, is it left or right, and compare it to \( - c / b \).
  4. set a = 1, b = 1, d = 0 and change c starting from zero going slowly to negative smaller values. Take note of the shift, is it left or right, and compare it to \( - c / b \).
  5. repeat 3 and 4 above for b = 2, 3 and 4.
  6. set a, b and c to non zero values and change d. What is the direction of the shift of the graph?
  7. What parameters affect the positions of the asymptotes? Explain algebraically.

More References and Links

Graphing Tangent Functions. A step by step tutorial on graphing and sketching tangent functions. The graph, domain, range and vertical asymptotes of these functions and other properties are examined.
Derivative of tan(x).
Trigonometric Functions.