Integrals Involving sin x , cos x and Exponential Functions

Tutorial to find integrals involving the product of   sin x   or   cos x   with exponential functions. Exercises with answers are at the bottom of the page.
All the integrals included in the examples belo are evaluated using Integration by Parts given by:
Integration by Parts Rule
The integration by parts helps in evaluating integral of product of functions of the form U dV/dx .

Examples

In what follows, C is the constant of integration.

Example 1

Evaluate the integral \[ \int \sin(x) e^x \, dx \] Solution to Example 1:
Let \( u = \sin(x) \) and \( \dfrac{dv}{dx} = e^x \) which gives \( u' = \cos(x) \) and \( v = \displaystyle \int e^x \, dx = e^x \).
Use the integration by parts Integration by Parts Rule as follows
integral of sin(x) e^x by parts
We apply the integration by parts to the term \( \displaystyle \int \cos(x)e^x \, dx \) in the expression above, hence
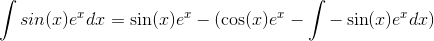
integral of sin(x) e^x by parts a second time
Simplify the above and rewrite as

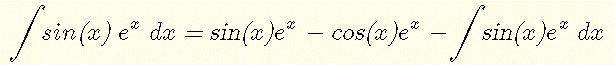
Simplify Integral Step 1
Note that the term on the right is the integral we are trying to evaluate, hence the above may be written as follows
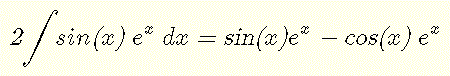
Simplify Integral Step 2
Hence the integral is given by
Simplify Integral Step 3

Example 2

Evaluate the integral

\[ \int \cos(2x) \, e^x \, dx \] Solution to Example 2:
Substitution: Let \( u = \cos(2x) \) and \( \dfrac{dv}{dx} = e^x \) which gives \( u' = - 2 \sin(2x) \) and \( v = \displaystyle \int e^x \, dx = e^x \) :
Apply the integration by parts: Integration by Parts Rule
\( \displaystyle \int \cos(2x) e^x \, dx = \cos(2x) \, e^x - \int -2 \sin(2x) e^x \, dx \)
= \( \cos(2x) \, e^x + 2 \int \sin(2x) \, e^x \, dx \)
Apply integration by parts to the term on the right
= \( \cos(2x) \, e^x + 2 ( \sin(2x)e^x - 2 \displaystyle \int \cos(2x)e^x \, dx ) \)
= \( \cos(2x) \, e^x + 2 \sin(2x) \, e^x - 4 \displaystyle \int \cos(2x)e^x \, dx \)
Note that the term on the right is related to the integral we are trying to evaluate, we can write that
\( 5 \displaystyle \int \cos(2x)e^x \, dx = \cos(2x) \, e^x + 2 \sin(2x) \, e^x \)
The given integral is evaluated as \[ \int \cos(2x) \, e^x \, dx = \dfrac{1}{5} e^x ( \cos(2x) + 2 \sin(2x) ) + C \]


Example 3

Evaluate the integral \[ \int \sin(3x + 2) \, e^{3x} \, dx \] Solution to Example 3:
Substitution: Let \( u = \sin(3x + 2) \) and \( \dfrac{dv}{dx} = e^{3x} \) which gives \( u' = 3 \cos(3x + 2) \) and \( v = \displaystyle \int e^{3x} \, dx = \dfrac{1}{3} e^{3x} \).
Apply the integration by parts
\( \displaystyle \int \sin(3x + 2) \, e^{3x} \, dx = \sin(3x + 2) \dfrac{1}{3} e^{3x} - \int \cos(3x + 2) \dfrac{1}{3} e^{3x} \, dx \)
Apply the integration by parts one more time to the term \( \int \cos(3x + 2) e^{3x} \, dx \)
\( \displaystyle \int \sin(3x + 2) e^{3x} \, dx = \dfrac{1}{3} \sin(3x + 2) e^{3x} - ( \cos(3x + 2) \dfrac{1}{3} e^{3x} + \int \sin(3x + 2) e^{3x} \, dx ) \)
Note that the term on the right is the integral to be evaluated, hence the above may be written as
\( 2 \displaystyle \int \sin(3x + 2) e^{3x} \, dx = \dfrac{1}{3} \sin(3x + 2) e^{3x} = \dfrac{1}{3} \sin(3x + 2) e^{3x} - ( \cos(3x + 2)\dfrac{1}{3} e^{3x} \)
Divide all terms by 2 and simplify \[ \int \sin(3x + 2) e^{3x} \, dx = \dfrac{1}{6} e^{3x} ( \sin(3x + 2) - \cos(3x + 2) ) + C \]


Example 4

Evaluate the integral \[ \int \cos(4x) \, e^{2x + 5} \, dx \]
Solution to Example 4:
Substitution: Let \( u = \cos(4x) \) and \( \dfrac{dv}{dx} = e^{2x + 5} \) and apply the integration by parts twice
\( \displaystyle \int \cos(4x) \, e^{2x + 5} \, dx = \cos(4x) \dfrac{1}{2} e^{2x + 5} + 2 \int \sin(4x) \, e^{2x + 5} \, dx \)
= \( \displaystyle \cos(4x) \dfrac{1}{2} e^{2x + 5} + 2 \{ \sin(4x) \dfrac{1}{2}e^{2x + 5} - 2 \int \cos(4x) \, e^{2x + 5} \, dx \} \)
The term on the right is the integral to be evaluated, hence \[ \int \cos(4x) \, e^{2x + 5} \, dx = \dfrac{1}{10} e^{2x + 5} ( \cos(4x) + 2 \sin(4x) ) + C \]


Exercises

Evaluate the following integrals.
1. \( \displaystyle\int \cos(x) \, e^x \, dx \)
2. \( \displaystyle \int \sin(2x) \, e^{3x} \, dx \)
3. \( \displaystyle \int \cos(-3x + 5) \, e^{5x} \, dx \)
4. \( \displaystyle \int \sin(-4x + 3) \, e^{-2x + 1} \, dx \)


Answers to Above Exercises

1. \( \dfrac{1}{2} e^x ( \cos(x) + \sin(x) ) + C \)
2. \( \dfrac{1}{13} e^{3x} ( 3 \sin(2x) - 2 \cos(2x)) + C \)
3. \( \dfrac{1}{34} e^{5x} ( 5 \cos(-3x + 5) - 3 \sin(-3x + 5) ) + C \)
4. \( \dfrac{1}{10} e^{-2x + 1} ( 2 \cos(-4x + 3) - \sin(-4x + 3) ) + C \)


More References and links

{ezoic-ad-1}
{ez_footer_ads}