Mean Value Theorem Problems

Problems related to the mean value theorem, with detailed solutions, are presented.

Mean Value Theorem: Review

If \( f \) is a function continuous on the interval \( [ a , b ] \) and differentiable on \( (a , b ) \) , then at least one real number \( c \) exists in the interval (a , b) such that
\( f'(c) = \dfrac{{f(b) - f(a)}}{{b - a}} \).
The mean value theorem expresses the relatonship between the slope of the tangent to the curve at \( x = c \) and the slope of the secant to the curve through the points (a , f(a)) and (b , f(b)).

Problem 1

Find a value of \( c \) such that the conclusion of the mean value theorem is satisfied for
\[ f(x) = -2x^3 + 6x - 2 \]
on the interval [-2 , 2]

Solution to Problem 1
\( f(x) \) is a polynomial function and is continuous and differentiable for all real numbers. Let us evalute \( f(x) \) at \( x = -2 \) and \( x = 2 \)
\( f(-2) = -2(-2)^3 + 6(-2) - 2 = 2 \)
\( f(2) = -2(2)^3 + 6(2) - 2 = - 6 \)
Evaluate \( \dfrac{{f(b) - f(a)}}{{b - a}} \)
\( \dfrac{{f(b) - f(a)}}{{b - a}} = \dfrac{{-6 - 2}}{{2 - (-2)}} = -2 \)
Let us now find \( f'(x) \).
\( f'(x) = - 6x^2 + 6 \)
We now construct an equation based on \( f'(c) = \dfrac{{f(b) - f(a)}}{{b - a}} \)
\( -6c^2 + 6 = -2 \)
Solve for \( c \) to obtain 2 solutions
\( c = 2 \sqrt{\dfrac{1}{3}} \) and \( c = - 2 \sqrt{\dfrac{1}{3}} \)
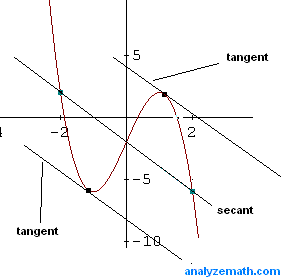
Below is shown the graph of \( f \), a secant and the two tangents corresponding to the two solutions found. The secant and the two tangents are parallel since their slopes are equal according to the mean value theorem.

curve with a secant and two tangent: mean value theorem.

Problem 2

Use the mean value theorem to prove that for any two real numbers \( a \) and \( b \), \[ | \cos a - \cos b| �‰� | a - b| \] Solution to Problem 2
Function \( \cos x \) is continuous and differentiable for all real numbers. Use the mean value theorem, using 2 real numbers \( a \) and \( b \) to write \[ (\cos x)' = \dfrac{{\cos a - \cos b}}{{a - b}} \] Take the absolute value of both sides \[ | (\cos x)' | = \left| \dfrac{{\cos a - \cos b}}{{a - b}} \right| \] \( (\cos x)' = - \sin x \), and therefore \( | (\cos x)' | �‰� 1 \)
Which gives \[ \left| \dfrac{{\cos a - \cos b}}{{a - b}} \right| �‰� 1 \] From the properties of absolute value, we have \[ \left| \dfrac{\cos a - \cos b}{a-b} \right| = \dfrac{|\cos a - \cos b|} { |a - b|} \] When combined with the above gives \[ \dfrac {| \cos a - \cos b |}{| a - b |} �‰� 1 \] Multiply both sides by | a - b | to obtain \[ |\cos a - \cos b | �‰� | a - b | \]