Derivative, Maximum, and Minimum of Quadratic Functions

Differentiation is used to analyze key properties of quadratic functions such as intervals of increase and decrease, local maxima, and local minima.

A - Quadratic Function in General Form

Quadratic functions in their general form are written as:

where \(a\), \(b\), and \(c\) are real numbers with \(a \neq 0\).

The first derivative of \(f\) is:

To determine the maximum or minimum points and intervals of increase or decrease, analyze the sign of \(f'(x)\). The derivative is positive if:

We consider two cases based on the sign of \(a\):

Case 1: \(a > 0\)

Dividing both sides of the inequality by \(2a > 0\), we get:

The table below summarizes the sign of \(f'(x)\) and whether \(f\) is increasing or decreasing:

Thus, the quadratic function has a minimum at \(\left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right)\), decreases on \((-\infty, -\dfrac{b}{2a})\), and increases on \(\left(-\dfrac{b}{2a}, +\infty\right)\).

Case 2: \(a < 0\)

Dividing both sides by \(2a < 0\) reverses the inequality:

The sign of \(f'(x)\) is analyzed using the following table:

In this case, the quadratic function has a maximum at \(\left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right)\), increases on \((-\infty, -\dfrac{b}{2a})\), and decreases on \(\left(-\dfrac{b}{2a}, +\infty\right)\).

B - Quadratic Function in Vertex Form

Quadratic functions in vertex form are written as:

where \(a \neq 0\), and \(h, k\) are real numbers.

The derivative is:

We analyze the sign of \(f'(x)\) by considering:

Case 1: \(a > 0\)

Dividing both sides by \(a > 0\):

Use the following table to analyze the sign:

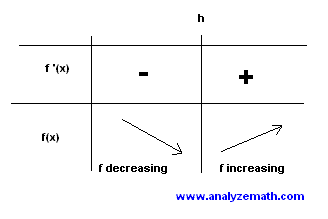
Therefore, the quadratic has a minimum at \((h, k)\), decreases on \((-\infty, h)\), and increases on \((h, +\infty)\).

Case 2: \(a < 0\)

Dividing both sides by \(a < 0\) reverses the inequality:

The sign of \(f'(x)\) is analyzed using:

Here, the quadratic has a maximum at \((h, k)\), increases on \((-\infty, h)\), and decreases on \((h, +\infty)\).

Example 1

Find the extremum (minimum or maximum) of the quadratic function:

Solution to Example 1

• First, find the derivative: \[ f'(x) = 4x - 8 \] The derivative changes sign at \(x = \dfrac{8}{4} = 2\). Since \(a=2 > 0\), \(f\) has a minimum at \((2, f(2)) = (2, -7)\).
• Function behavior:
  • Decreasing on \((-\infty, 2)\)
  • Increasing on \((2, +\infty)\)
• See the graph below confirming this result:

Example 2

Find the extremum of the quadratic function:

Solution to Example 2

• The derivative is: \[ f'(x) = -2(x + 3) \] The derivative changes sign at \(x = -3\). Since \(a = -1 < 0\), \(f\) has a maximum at \((-3, 1)\).
• Function behavior:
  • Increasing on \((-\infty, -3)\)
  • Decreasing on \((-3, +\infty)\)
• See the graph below:

Exercises on Properties of Quadratic Functions

For each quadratic function below, find the extremum (minimum or maximum), the interval of increase, and the interval of decrease:

1. \( f(x) = x^2 + 6x \)
2. \( f(x) = -x^2 - 2x + 3 \)
3. \( f(x) = x^2 - 5 \)
4. \( f(x) = -(x - 4)^2 + 2 \)
5. \( f(x) = -x^2 \)

Answers to the Exercises

• a) Minimum at \((-3, -9)\). Decreasing on \((-\infty, -3)\), increasing on \((-3, +\infty)\).
• b) Maximum at \((-1, 4)\). Increasing on \((-\infty, -1)\), decreasing on \((-1, +\infty)\).
• c) Minimum at \((0, -5)\). Decreasing on \((-\infty, 0)\), increasing on \((0, +\infty)\).
• d) Maximum at \((4, 2)\). Increasing on \((-\infty, 4)\), decreasing on \((4, +\infty)\).
• e) Maximum at \((0, 0)\). Increasing on \((-\infty, 0)\), decreasing on \((0, +\infty)\).

More on Applications of Differentiation

See more about applications of differentiation.