Question 1
For the function f(x) = (x + 3)(x - 2) 3 find
a) the interval(s) of increase and decrease of f,
b) the value(s) of x for which f has a local maximum and minimum,
c) and the interval of concavity and inflection point(s).
Solution to Question 1:
-
a) We first find the first derivative f '
f '(x) = (x - 2) 3 + 3(x + 3)(x - 2) 2
= (x - 2) 2(4x + 7)
-
f'(x) has zeros at
are x = 2 and x = - 7/4
-
The table of sign of f '(x) is shown below



-
Using the table, f is decreasing on the interval
(-infinity , - 7/3)
-
and increasing on the interval
(- 7/3 , +infinity)
-
b) f has a local minimum at x = - 7/3. Note that although f '(2) = 0, there is no local extremum at x = 2. This is because f ' (x) does not change sign at x = 2.
-
c) We now calculate f"(x)
f"(x) = 2(x - 2)(4x + 7) + 4(x - 2) 2
= 6(x - 2)(2x + 1)
-
The sign table of f"(x)is shown below
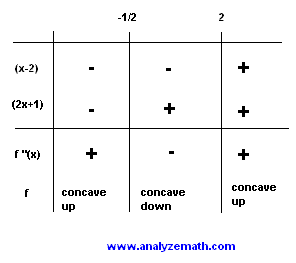


-
Using the above table, we can say that the graph of f is concave up on the intervals (-infinity , -1/2) and (2 , +infinity) and concave down on the interval (-1/2 , 2).
Question 2
Given f(x) = e (x 2 - x), find
a) the interval(s) of increase and decrease of f,
b) value(s) of x for which f has a local extremum,
c) the interval(s) of concavity and any inflection point(s).
Solution to Question 2:
-
Find f '(x)
a) f '(x) = (2x - 1) e (x 2 - x)
-
f '(x) has one zero at x = 1/2. The sign table of f '(x) is shown below
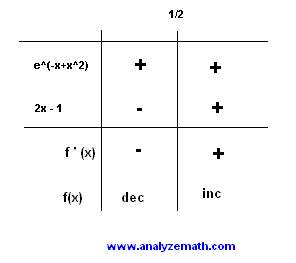


-
f is decreasing on (-infinity , + 1/2) and increasing on (1/2 , +infinity).
-
b) Since x = 1/2 is a critical value and f ' changes sign at x = 1/2, there is a local minimum at x = 1/2.
-
c) We first calculate the second derivative f" of f.
f"(x) = 2 e (x 2 - x) + (2x-1)(2x-1)e (x 2 - x)
= [ 2 + (2x+1)2 ] e (x 2 - x)
-
The second derivative f" is always positive. Hence the graph of f is concave up on (-infinity , +infinity) and since f" does not change sign, the graph of f has no point of inflection.
| 1
| 2
| 3
| 4
| 5
|
More on calculus
questions with answers, tutorials and problems .
|






