Derivative of Even and Odd Functions
Questions, with answers, explanations and proofs, on derivatives of even and odd functions are presented.
Questions with Solutions
Question 1
The graph of an even function f is shown below.
Assume that function f is differentiable everywhere, which of the graphs A), B), C) or D) is the graph of the first derivative of f?
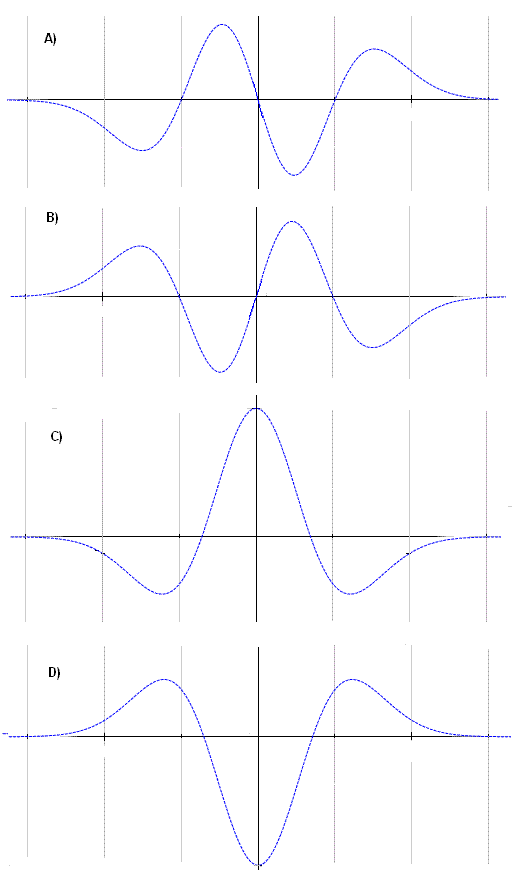
Solution to Question 1: The given function is even, hence
f(x) = f(-x)
Differentiate the two sides of the above equaltion.
df/dx = d(f(-x))/dx
To differentiate f(-x), we use the chain rule formula as follows:
Let u = - x, hence d(f(-x))/dx = df(u)/du . du/dx = f '(u) . (-1) = - f '(-x)
Substituting in df/dx = d(f(-x))/dx, we obtain
f '(x) = - f '(- x).
f '(- x) = - f '(x) and therefore this is the proof that the derivative of an even function is an odd function.
Analyzing the 4 graphs A), B), C) and D), only A) and B) are odd. Analyzing the graph of f; f is a decreasing function from the maximum on the left to the origin (0,0). Hence in this interval the derivative must be negative. Graph B) fulfills this condition and therefore the answer is B)
Question 2
The graph of an odd function f is shown below.
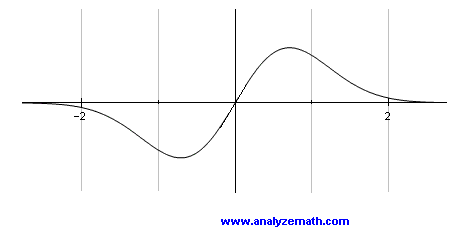
Assume that function f is differentiable everywhere, which of the graphs A), B), C) or D) is the graph of the first derivative of f?
Solution to Question 2:
The given function is odd, hence
f(x) = - f(-x)
Differentiate the two sides of the above equaltion.
df/dx = - d(f(-x))/dx
Use the chain rule formula to differentiate f(-x), we
Let u = - x, hence d(f(-x))/dx = df(u)/du . du/dx = f'(u) . (-1) = - f '(-x)
Substituting in df/dx = - d(f(-x))/dx, we obtain
f '(x) = - ( - f '(- x)) = f '(-x).
f '(- x) = f '(x) and therefore this is the proof that the derivative of an odd function is an even function.
Analyzing the 4 graphs A), B), C) and D), only C) and D) correspond to even functions. Analyzing the graph of f; f is an increasing function around the origin. Hence around the origin, the derivative must be positive. Graph C) fulfills this condition and therefore the answer is C)
