Exponential Functions

This page presents a detailed study of exponential functions using tables of values and graphs. Key properties such as domain, range, horizontal asymptotes, and intercepts are discussed. We also investigate the conditions under which an exponential function increases or decreases.

Definition of the Exponential Function

The basic exponential function is defined by

where the base \( B \) satisfies \( B > 0 \) and \( B \neq 1 \).

The domain of the exponential function \( f \) defined above is the set of all real numbers.

Example 1: Exponential Functions with Base Greater Than 1

The table below shows values of the exponential functions \( 2^x \), \( 4^x \), and \( 7^x \).

Example 2: Exponential Functions with Base Between 0 and 1

The table below shows values of the exponential functions \( 0.2^x \), \( 0.5^x \), and \( 0.8^x \).

Properties of Exponential Functions

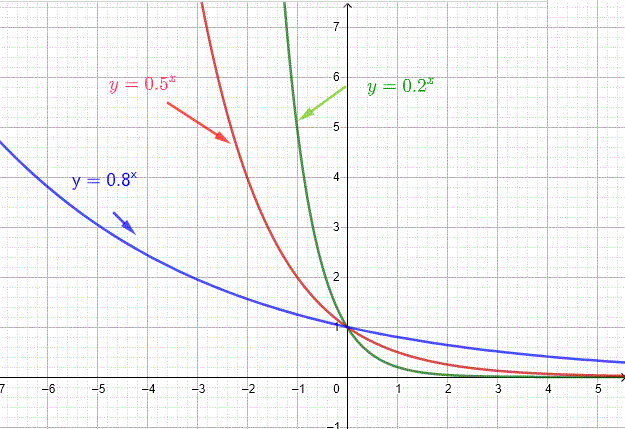
From the tables and graphs above, we conclude:

1. The domain of \( f(x) = B^x \) is all real numbers.
2. If \( B > 1 \), then \( f(x) = B^x \) is increasing: \[ \lim_{x \to +\infty} B^x = +\infty, \qquad \lim_{x \to -\infty} B^x = 0 \]
3. If \( 0 < B < 1 \), then \( f(x) = B^x \) is decreasing: \[ \lim_{x \to +\infty} B^x = 0, \qquad \lim_{x \to -\infty} B^x = +\infty \]
4. The horizontal asymptote of all exponential functions is \( y = 0 \).
5. All exponential functions satisfy \( f(0) = 1 \) and therefore have a y-intercept at \( (0,1) \), but no x-intercept.
6. The range of \( f(x) = B^x \) is \[ (0, +\infty) \]

See also: Finding the Range of Exponential Functions

Writing Exponentials Using the Natural Base

Let \( f(x) = B^x \). Since \( B = e^{\ln B} \), we have

Thus,

In calculus, natural exponentials are preferred because their derivatives and integrals are especially simple.

Further Reading

• Graphing Exponential Functions
• Natural Logarithm
• Natural Exponential Function
• Exponential and Logarithmic Functions