Applications of Functions

Examples of applications of functions where quantities such area, perimeter, chord are expressed as function of a variable.

Problem 1

A right triangle has one side x and a hypotenuse of 10 meters. Find the area of the triangle as a function of x.

Solution to Problem 1
If the sides of a right triangle are x and y, the area A of the triangle is given by
A = ( 1 / 2) x * y
We now need to express y in terms of x using the hypotenuse, side x and Pythagora's theorem
10 2 = x 2 + y 2
y = sqrt [100 - x 2 ]
Substitute y by its expression in the area formula to obtain
A(x) = ( 1 / 2) x sqrt [100 - x 2 ]



Problem 2

A rectangle has an area equal to 100 cm2 and a width x. Find the perimeter as a function of x.

Solution to Problem 2
If x and y are the dimensions of the rectangle, using the formula of the area we obtain
100 = x * y
The perimetr P is given by
P = 2(x + y)
Solve the equation 100 = x * y for y and substitute y in the formula for the perimeter
P(x) = 2(x + 100 / x)



Problem 3

Find the area of a square as a function of its perimeter x.

Solution to Problem 3
The area of a square of side L is given by
A = L 2
The perimeter x of a square with side L is given by
x = 4 L
Solve the above for L and substitute in the area formula A above
A(x) = (x/4) 2 = x 2 / 16



Problem 4

A right circular cylinder has a radius r and a height equal to twice r. Find the volume of the cylinder as a function of r.

Solution to Problem 4
The volume V of a right circular cylinder is given by
V = (area of base of cylinder) * (height of cylinder)
= Pi * r 2 * (2 r)
= 2 Pi r 3



Problem 5

Express the length L of the chord of a circle, with given radius r = 10 cm , as a function of the arc length s.(see figure below).
figure problem 5

Solution to Problem 5
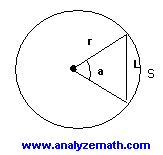
Using half the angle a, we can write
sin(a / 2) = (L / 2) / r
Substitute r by 10 and solve for L
L = 20 sin(a / 2)
The relationship between arc length s and central angle a is
s = r a = 10 a
Solve for a
a = s / 10
Substitute a by s / 10 in L = 20 sin(a / 2) to obtain
L = 20 sin ( (s / 10) / 2 )
= 20 sin ( s / 20)



Problem 6

Express the distance d = d1+ d2, in the figure below, as a function of x.
figure problem 6

Solution to Problem 6
d1 is the length of the hypotenuse of a right triangle of sides x and 3, hence
d1 = sqrt[ 3 2 + x 2 ]
d2 is the length of the hypotenuse of a right triangle of sides 7 - x and 5, hence
d2 = sqrt[ 5 2 + (7 - x) 2 ]
d = d1 + d2 is given by
d = sqrt[ 9 + x 2 ] + sqrt[ 25 + (7 - x) 2 ]



Exercises

1. Express the area A of a disk in terms of its circumference C.
2. The width of a rectangle is w. Express the area A of this rectangle in terms of its perimeter P and width w.

Solutions to above exercises
1. A = C 2 / (4 Pi)
2. A = (1/2) w (P - 2w)

More tutorials on functions.