Solutions to Questions Multiply, Divide, Simplify Rational Expressions

Detailed solutions to questions in How to multiply, divide and simplify rational expressions are presented.

Rules of multiplication, division and simplification of rational expressions?
We multiply two rational expressions by multiplying their numerators and denominators as follows:
1)

multiply rational expressions

We divide two rational expressions by multiplying the first by the reciprocal of the second as follows:
2)
divide rational expressions

Simplify the rational expressions

a) simplify expressions question a
Solution:
The division of two rational expressions is done by multiplying the first by the reciprocal of the second as follows (see division rule above). Hence
solution part 1 to question a
Multiply numerators and denominators (multiplication rule).
solution part 2 to question a
Factor the terms 6x-9 included in the denominator as follows:
6x - 9 = 3(2x - 3)
and use the factored form in the rational expression
solution part 3 to question a
simplify
solution part 4 to question a



b) simplify expressions question b
Solution:
Apply the multiplication rule (see above)
solution part 1 to question b
Factor terms in the numerator and the denominator:
10 x + 10 = 10(x + 1) ; 2 x + 2 = 2(x + 1) ; 4 x - 10 = 2(2x - 5)
and use in factored form
solution part 2 to question b
Simplify if possible
solution part 3 to question b


c) simplify expressions question c
Solution:
The division of two rational expressions is done by multiplying the first rational expression by the reciprocal of the second rational expression as follows (see division rule above). Hence
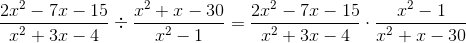
solution part 1 to question c
Multiply numerators and denominators (multiplication rule) but do not expand as we might be able to simplifty.
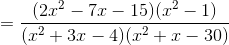
solution part 2 to question c
factor terms in the numerator and denominator if possible.
2 x 2 - 7 x - 15 = (2x + 3)(x - 5) ; x 2 - 1 = (x - 1)(x + 1)
x 2 + 3 x - 4 = (x + 4)(x - 1) ; x 2 + x - 30 = (x + 6)(x - 5)
and use in rational expression
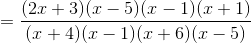
solution part 3 to question c
and simplify.
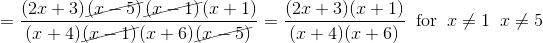
solution part 4 to question b



d) simplify expressions question d

Solution:
We have the multiplication of two rational expressions inside the parentheses and we then apply multiplication rule. We also have a division by a rational expression which is done by multiplying by the reciprocal. Hence
solution part 1 to question d
Multiply numerators and denominators (multiplication rule) but do not expand as we might be able to simplify.
solution part 2 to question d
Factor terms in numerator and denominator if possible and use in rational expression
x 2 - 4 = (x - 2)(x + 2) and x 2 - 1 = (x - 1)(x + 1)
solution part 3 to question d
Simplify
solution part 4 to question d



e) simplify expressions question e
Solution:
The division of two rational expressions is done by multiplying the first rational expression by the reciprocal of the second rational expression as follows (see division rule above). Hence
solution part 1 to question e
Multiply numerators and denominators (multiplication rule) but do not expand.
solution part 2 to question e
factor term x 3 - 27 in the numerator and use it.
x 3 - 27 = (x - 3)(x 2 + 3 x + 9)
and use in rational expression
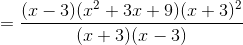
solution part 3 to question e
and simplify.
solution part 4 to question e



f) simplify expressions question f
Solution:
Apply the multiplication rule (see above)
solution part 1 to question f
Factor terms in the numerator and the denominator:
2 y - x = 2 (y - (1/2) x) ; 4 x + 6 y = 2(2 x + 3) ; 4 x 2 - 9 y 2 = (2x - 3y)(2x + 3y)
and use in factored form
solution part 2 to question f
Simplify if possible
solution part 3 to question f

More Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
More High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
More Primary Math (Grades 4 and 5) with Free Questions and Problems With Answers
Author - e-mail
Home Page