Geometry Problems with Solutions for Grade 12
Explore a collection of grade 12 geometry problems with detailed solutions designed to help you think critically and develop problem-solving skills. If a problem seems challenging, don’t give up too quickly—take your time, explore different approaches, and, if possible, collaborate with others. Group discussions can spark new ideas and enhance learning. Remember, the best way to grow is by tackling problems that initially seem difficult!
Problem 1
In the triangle \( ABC \) sides \( AB \) and \( CB \) have equal lengths and the measure of angle \( \angle ABC \) is equal to \( 36^\circ \). What is the measure of angle \( \angle BOC \) where O is the center of the circle? .
.
Triangle \( ABC \) has two sides with equal length and therefore is an isosceles triangle with base AC. The measure of angle \( \angle BAC \) is given by:
\[ \angle BAC = \dfrac{180^\circ - 36^\circ}{2} = 72^\circ \] Angle \( \angle BOC \) is a central angle and \( \angle BAC \) is an inscribed angle and both angles intercept the same arc; hence: \[ \text{Measure of } \angle BOC = 2 \times \text{Measure of } \angle BAC = 144^\circ \]Problem 2
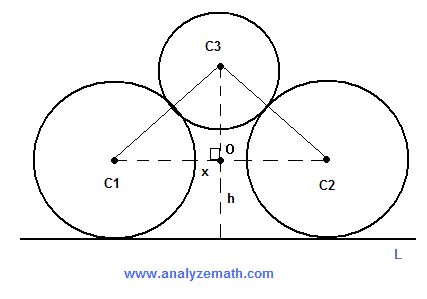
Circles C1 and C2 have equal radii and are tangent to that same line L. Circle C3 is tangent to C1 and C2. \( x \) is the distance between the between the centers of C1 and C2. Find the distance \( h \), from the center of C3 to line L, in terms of \( x \) and the radii of the three circles.
 .
.
Let \( R_1, \; R_2 \) and \( R_3 \) be the radii of circles C1, C2 and C3 with \( R_1 = R_2 = R \).
 .
.
Let \( C3O \) be the distance from C3 to the segment C1, C2. Hence \[ h = C3O + R \quad (I) \]
Apply Pythagoras' theorem applied to triangle C3 O C1 \[ C3O^2 + \left(\dfrac{x}{2}\right)^2 = (R + R_3)^2 \]
which gives \[ C3O = \sqrt{(R + R_3)^2 - \left(\dfrac{x}{2}\right)^2} \]
Using (I), we obtain \[ h = R + C_3O = R + \sqrt{(R + R_3)^2 - \left(\dfrac{x}{2}\right)^2} \]
Problem 3
All three circles are tangent to the same line and to each other. Circles C2 and C3 have equal radii. Find the radius of C2 if the radius of C1 is equal to 10 cm.
 .
.
Let \( r \), \( R_2 \), and \( R_3 \) be the radii of circles \( C1 \), \( C2 \), and \( C3 \) respectively, with \( R_2 = R_3 = R \).
 .
.
Problem 4
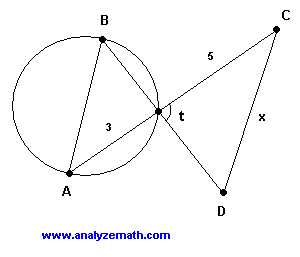
\( CD \) is parallel to \( AB \) and the measure of angle \( t \) is equal to \( 90^\circ \). Find the area of the circle in terms of \( x \).
 .
.
Angles \( \angle BtA \) and \( \angle CtD \) are vertical and therefore
\[ \angle BtA = 90^\circ \] Since \( \angle BtA = 90^\circ \), \( AB \) is the diameter of the circle using the converse of Thales' theorem.Since \( CD \) is parallel to \( AB \) Triangle \( BtA \) and triangle \( CtD \) are similar and hence the proportionality of the corresponding sides gives: \[ \dfrac{3}{5} = \dfrac{AB}{x} \] Solve for the diameter \( AB \) \[ AB = \dfrac{3x}{5} \quad \] \[ \text{radius} = \dfrac{AB}{2} = \dfrac{3x}{10} \] \[ \text{area} = \pi \times \text{radius}^2 = \pi \left(\dfrac{3x}{10}\right)^2 = 0.09 \pi x^2 \]
Problem 5
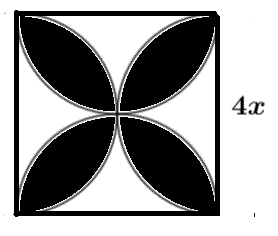
The shaded region below is the common area to four semicircles whose diameters are the sides of the square with side length \(4 x \). Find the area of the shaded region in terms of \( x \).
 .
.
Let us split the large square into four small squares as shown in the image.
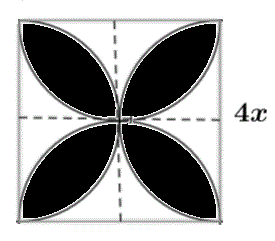
Let us consider one small square, the bottom left one for example. The square below has a side length of \( 2x \), which is half of the given square. Part of this square is shaded, while the other part is not shaded. Let us find the area of the non-shaded (white) part. The shaded part is a quarter of a disk (circle).
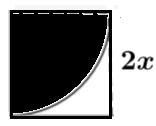 .
\[
\text{Area of non-shaded region} = \text{area of the square - 1/4 of the area of the circle} = (2x)^2 - \dfrac{1}{4} \pi (2x)^2
\]
.
\[
\text{Area of non-shaded region} = \text{area of the square - 1/4 of the area of the circle} = (2x)^2 - \dfrac{1}{4} \pi (2x)^2
\]
If we go back to the given shape in problem 5, the total area of the non-shaded part is \( 8 \) times the non-shaded area in the image of the small square above, which is given by \( (2x)^2 - \dfrac{1}{4} \pi (2x)^2 \).
The area A of the shaded part in the shape of problem 5 is given by: \[ A = \text{Total area of the large square} - \text{Total non-shaded area} \] \[ = (4x)^2 - 8 \left[ (2x)^2 - \dfrac{1}{4} \pi (2x)^2 \right] \] \[ = 16x^2 \left( \dfrac{\pi}{2} - 1 \right) \]
Problem 6
A small circle od radius \( r \) and a large circle od radius \( R \) are concentric (have same center). The length of the chord tangent to the smaller circle is equal to \( 20 \) mm. What is the area of the ring (shaded area) between the two circles ?
 .
.
The right triangle in the image has a hypotenuse whose length is \( R \), one side \( r \) and the second side half of the cord whose length is \( 20 / 2 \) mm.
 .
.
Use the Pythagorean theorem
\[ R^2 = r^2 + 10^2 \quad (I) \] The area \( A \) of the ring is found by suntracting the area of the small circle from that of the large circle: \[ A = \pi (R^2 - r^2) \quad (II) \] \] The first equation \( I \) gives \[ R^2 - r^2 = 10^2 = 100 \] Substitute \( (II) \) to obatin the area of the ring \[ A = 100 \pi \] \]Problem 7
Find \( b \), \( c \) and \( d \) so that the quadrilateral is a parallelogram with area equal to 80 square units.
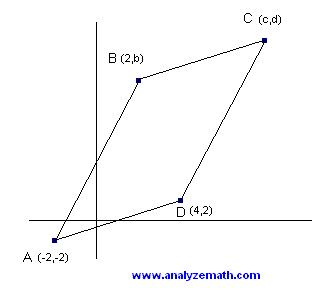 .
.
The area of a parallelogram may be calculated using the cross product of vectors \(\mathbf{AB}\) and \(\mathbf{AD}\) as follows: \[ \text{Area} = \left| \mathbf{AB} \times \mathbf{AD} \right| \] where \(\mathbf{AB}\) and \(\mathbf{AD}\) are 3-dimensional vectors with the \( z \) component equal to zero so that we can perform the cross product \( \mathbf{AB} \times \mathbf{AD} \).
Each vectors is calculated using the coordinates of the points defining the vector as follows: \[ \mathbf{AB} = \langle 2 - (-2) , b - (- 2), 0 - 0 \rangle = \langle 4 , b +2, 0 \rangle \] \[ \mathbf{AD} = \langle 4-(-2), 2 - (-2) , 0 \rangle = \langle 6, 4, 0 \rangle \] Computing the magnitude of the cross product: \[ \left| \langle 4, b+2, 0 \rangle \times \langle 6, 4, 0 \rangle \right| = 80 \] The determinant form of the cross product in three dimensions is: \[ \mathbf{AB} \times \mathbf{AD} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 4 & b+2 & 0 \\ 6 & 4 & 0 \end{vmatrix} \] Expanding along the first row: \[ = \mathbf{i} \begin{vmatrix} b+2 & 0 \\ 4 & 0 \end{vmatrix} - \mathbf{j} \begin{vmatrix} 4 & 0 \\ 6 & 0 \end{vmatrix} + \mathbf{k} \begin{vmatrix} 4 & b+2 \\ 6 & 4 \end{vmatrix} \] which gives \[ \mathbf{AB} \times \mathbf{AD} = (4 - 6b) \mathbf{k} \] Taking the magnitude: \[ |4 - 6b| = 80 \] Solving for \( b \): \[ 4 - 6b = 80 \quad \text{or} \quad 4 - 6b = -80 \] \[ b = -\dfrac{38}{3}, \quad b = 14 \] Since point \( B(2, b) \) is in the first quadrant, we choose \( b = 14 \). Since \( ABCD \) is a parallelogram, we have: \[ \mathbf{AB} = \mathbf{DC} \] Thus, \[ \mathbf{AB} = \langle 4, 16, 0 \rangle \] \[ \mathbf{DC} = \langle c - 4, d - 2, 0 \rangle \] Equating corresponding components: \[ c - 4 = 4, \quad d - 2 = 16 \] Solving: \[ c = 8, \quad d = 18 \] Hence : \( b = 14 \) , \( c = 8\) and \( d = 18 \)
Problem 8
A right triangle is shown below. Find the lengths \( x \), \( y \) and \( z \).
 .
.
to find \( x = \dfrac{27}{5} \) and \( y = \dfrac{48}{5} \)
Use equation \( (I) \) to find \( z \) \[ \left(\dfrac{48}{5}\right)^2 + z^2 = 12^2 \] \[ z^2 = 12^2 - \left(\dfrac{48}{5}\right)^2 = \dfrac{1296}{25} \] Hence \[ z = \dfrac{36}{5} \] The values of \( x, y \) and \( z \) are \[ x = \dfrac{27}{5}, \quad y = \dfrac{48}{5}, \quad z = \dfrac{36}{5} \]
Problem 9
A rectangle is shown below. Find the length \( x \).
 .
.
Split the given rectangle into 4 other rectangles as shown.
 .
.
Pythagoras' theorem applied to the top-left right triangle of side \( a \) and hypotenuse \( 4 \) gives: \[ a^2 + c^2 = 4^2 \quad (I) \] Pythagoras' theorem applied to the bottom-left right triangle gives: \[ b^2 + c^2 = x^2 \quad (II) \] Pythagoras' theorem applied to the bottom-right right triangle. \[ b^2 + d^2 = 5^2 \quad (III) \] Pythagoras' theorem applied to the top-right right triangle. \[ a^2 + d^2 = 6^2 \quad (IV) \] Subtracting equations \( (II) \) from \( (I) \) \[ a^2 - b^2 = 4^2 - x^2 \] Subtracting equations \( (III) \) from \( (IV) \) \[ a^2 - b^2 = 6^2 - 5^2 \] Substitute \( a^2 - b^2 = 4^2 - x^2 \) in the above equation to obatin: \[ 4^2 - x^2 = 6^2 - 5^2 \] Solve for \( x \). \[ x = \sqrt{5} \]
Problem 10
The two circles below have equal radii of \( 4 \) units each and the distance between their centers is \( 6 \) units. Find the area of the shaded region (common region to the two circles).
 .
.
Because of the symmetry, the shaded region may be considered as made up of two equal (in area) regions. The area of the left half of the shaded region is given by the area of the sector \( BOC \) minus the area of the triangle \( BOC \).

More References and Links
- High School Maths (Grades 10, 11 and 12) - Free Questions and Problems With Answers
- Grade 12 Math Practice Test
- Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
- High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
- Primary Math (Grades 4 and 5) with Free Questions and Problems With Answers
- Home Page