Intermediate Algebra: Linear Equations, Slopes,
and Practical Applications with Step-by-Step Solutions

This page offers a collection of intermediate algebra problems focused on slopes of lines and linear equations, complete with detailed solutions. These problems include practical applications to help you understand and apply algebra concepts effectively.

Questions 1

Find the slopes of the lines given by the following equations:

  1. \( 2x + 3y = 2 \)
  2. \( y = 2 \)
  3. \( x = 4 \)

Solution:

  1. Solve equation for \( y \): \[ y = \dfrac{-2}{3}x + \dfrac{2}{3} \] \[ \text{Slope} = \dfrac{-2}{3} \]
  2. The slope of a horizontal line such as \( y = 2 \) is equal to \( 0 \).
  3. The slope of a vertical line such as \( x = 4 \) is undefined.

Questions 2

Find the slopes of the lines through the points A and B given by:

  1. \( A(2 , 1) ,\ B(3 , 4) \)
  2. \( A(3 , -4) ,\ B(5 , -4) \)
  3. \( A(2 , -6) ,\ B(2 , -7) \)

Solution:

  1. Slope: \( \dfrac{4 - 1}{3 - 2} = \dfrac{3}{1} = 3 \)
  2. Slope: \( \dfrac{-4 - (-4)}{5 - 3} = \dfrac{0}{2} = 0 \), the line through \( A(3, -4) \) and \( B(5, -4) \) is a horizontal line.
  3. Slope: \( \dfrac{-7 - (-6)}{2 - 2} = \dfrac{-1}{0} \), which is undefined. The line through \( A(2, -6) \) and \( B(2, -7) \) is a vertical line.

Questions 3

Find the slopes of the lines

  1. parallel to the line whose equation is given by \(5x - 3y = -3\)
  2. perpendicular to the line whose equation is given by \(-4x - 8y = -3\)
  3. parallel to the line whose equation is given by \(x = 2\)
  4. perpendicular to the line whose equation is given by \(x = -9\)
  5. parallel to the line whose equation is given by \(y = 3\)
  6. perpendicular to the line whose equation is given by \(x = 0\)

Solution:

  1. Rewrite in slope-intercept form \(y = mx + b\): \[ -3y = -5x - 3 \implies y = \dfrac{5}{3}x + 1 \] Slope of the given line: \[ m = \dfrac{5}{3} \] So, slope of lines parallel to it is: \[ \boxed{\dfrac{5}{3}} \]
  2. Rewrite equation in slope-intercept form: \[ -8y = 4x - 3 \implies y = -\dfrac{1}{2}x + \dfrac{3}{8} \] Slope of the given line: \[ m = -\dfrac{1}{2} \] Slope of perpendicular lines is the negative reciprocal: \[ m_{\perp} = -\dfrac{1}{ -\dfrac{1}{2}} = 2 \] So, slope of lines perpendicular to it is: \[ \boxed{2} \]
  3. Given equation: \[x = 2\] This is a vertical line, slope is undefined. Lines parallel to vertical lines are also vertical, so slope is undefined.
  4. Given equation: \[x = -9\] This is a vertical line, slope is undefined. Lines perpendicular to vertical lines are horizontal, slope = 0. So slope of perpendicular lines is: \[ \boxed{0} \]
  5. Given equation:: \[y = 3\] This is a horizontal line, slope = 0. Lines parallel to horizontal lines have slope = 0. So slope of lines parallel to it is: \[ \boxed{0} \]
  6. Given equation:: \[x = 0\] This is a vertical line (the y-axis), slope is undefined. Lines perpendicular to vertical lines are horizontal, slope = 0. So slope of lines perpendicular to it is: \[ \boxed{0} \]

Questions 4

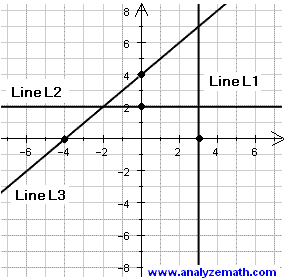Find the slope of each of the lines graphed below. intermediate algebra problem 4, slopes.

Solution:

  1. \( L_1 \) is a vertical line and its slope is undefined.
  2. \( L_2 \) is a horizontal line and its slope is equal to \( 0 \).
  3. The slope of \( L_3 \) may be found using the \( x \) inytercept at \( (-4,0) \) and the \( y \) intercepts at \( (0,4) \): \[ \text{slope} = \dfrac{4 - 0}{0 - (-4)} = 1 \]

Questions 5

Find the value of \( k \) so that the slope of the line through the points \( (4 , 2) \) and \( (k , 6) \) is equal to \( -2 \).

Solution:

Slope through the two points is given by: \[\dfrac{6 - 2}{k - 4}\] and is equal to \( -2 \) \[\dfrac{6 - 2}{k - 4} = - 2\] Simplify: \[\dfrac{4}{k - 4} = - 2\] Which, by cross product, gives \[ 4 = -2 (k - 4) \] Solve for \(k\) : \(k = 2\)

Questions 6

Find the value of \( k \) so that the lines with equations \( 2y + k x = 2 \) and \( 3x - 2y = 6 \) have equal slopes.

Solution:

Write the equation \[2y + kx = 2\] in slope-intercept form and find its slope \(m\). \[ 2y = -kx + 2 \] \[ y = -\dfrac{k}{2}x + \dfrac{1}{2} \] Slope \(m = -\dfrac{k}{2}\)

Write the equation \[3x - 2y = 6\] in slope-intercept form and find its slope \(s\). \[ -2y = -3x + 6 \] \[ y = \dfrac{3}{2}x - 3 \] Slope \(s = \dfrac{3}{2}\)

Set equal slopes: \[ -\dfrac{k}{2} = \dfrac{3}{2} \] Solve the above equation for \(k\): \[ k = -3 \]

Questions 7

Find the value of \( k \) so that the lines with equations \( -3 y + 2 x = 4 \) and \( k x + 2y = 3 \) are perpendicular.

Solution:

Write the equation \(-3y + 2x = 4\) in slope-intercept form and find its slope \(m\).
\[ -3y = -2x + 4 \]
\[ y = \dfrac{2}{3}x - \dfrac{4}{3} \] Slope: \(m = \dfrac{2}{3}\)

Write the equation \(kx + 2y = 3\) in slope-intercept form and find its slope \(s\).
\[ 2y = -kx + 3 \]
\[ y = -\dfrac{k}{2}x + \dfrac{3}{2} \]
Slope: \(s = -\dfrac{k}{2}\)

Perpendicular lines satisfy: \[ m \times s = -1 \] Substitute \(m\) and \(s\):
\[ \left(\dfrac{2}{3}\right) \times \left(-\dfrac{k}{2}\right) = -1 \] Solve for \(k\): \[ k = 3 \]

Questions 8

The oil consumption of a certain country was \( 330 \) thousands barrels per day in 2004 and \( 450 \) thousands barrels per day in 2006. Assume that the oil consumption in this country increases linearly and estimate the oil consumption in 2015.

Solution:

Oil Consumption Over Time

Let \( t \) be the number of years after 2004; hence \( t = 0 \) in 2004. The oil consumption \( C \) increases linearly with time \( t \), which may be written as: \[ C = mt + C_0 \]

In 2004 (corresponding to \( t = 0 \)), we have \( C = 330 \). Hence, the equation becomes:

\[ 330 = m \cdot 0 + C_0 \quad \Rightarrow \quad C_0 = 330 \]

So the equation becomes: \[ C = mt + 330 \]

The year 2006 corresponds to \( t = 2006 - 2004 = 2 \), and \( C = 450 \). Substituting into the equation:

\[ 450 = m \cdot 2 + 330 \] Solving for \( m \): \[ m = \dfrac{450 - 330}{2} = 60 \] The year 2015 corresponds to \( t = 2015 - 2004 = 11 \); hence the consumption in 2015 is given by:

\[ C = 60 \cdot 11 + 330 = 990 \text{ thousand barrels per day} \]

Questions 9

A family spent $\(3600\) on food last year and $\(3000\) the year before the last. Assume that the spending on food of this family increases linearly and estimate their spending on food for this year.

Solution:

Let us denote the spending two years ago as: \[ S_0 = \$3000 \] The spending last year was: \[ S_1 = \$3600 \] So the yearly increase is: \[ \Delta S = S_1 - S_0 = 3600 - 3000 = \$600 \] Assuming a linear increase, the spending this year would be: \[ S_2 = S_1 + \Delta S = 3600 + 600 = \$4200 \] Estimated spending this year: \$4200

Questions 10

To convert the measure of temperature given in degrees Fahrenheit \( T_f \) into degrees Celsius \( T_c \), you may use the formula given by: \[ T_c = \dfrac{5}{9}(T_f - 32) \] If the temperature of an item increases by 9 degrees Fahrenheit, by how many degrees Celsius has the temperature of this item increased?

Solution:

Using the formula \( T_c = \dfrac{5}{9}(T_f - 32) \), a change of \( \Delta T_f \) in Fahrenheit, gives a corresponding change in Celsius \( \Delta T_c \) given by: \[ \Delta T_c = \dfrac{5}{9} \Delta T_f \] Substitute \( \Delta T_f = 9 \): \[ \Delta T_c = \dfrac{5}{9} \times 9 = 5 \] So, the temperature increases by 5 degrees Celsius.

Questions 11

To convert the measure of temperature given in degree Celsius \( T_c \) into degree Fahrenheit, you may use the formula given by: \[ T_f = \dfrac{9}{5} T_c + 32 \]

If the temperature of an item increases by 10 degrees Celsius, by how many degrees Fahrenheit has the temperature of this item increased?

Solution:

Using the formula \( T_f = \dfrac{9}{5} T_c + 32 \), a change \( \Delta T_c \) in Celsius , gives a corresponding change in Fahrenheit \( \Delta T_f \) given by:

\[ \Delta T_f = \dfrac{9}{5} \Delta T_c \]

Substitute \( \Delta T_c = 10 \): \[ \Delta T_f = \dfrac{9}{5} \times 10 = 18 \] The temperature increases by \( \boxed{18} \) degrees Fahrenheit.

More References and Links

Algebra Questions and problems