Orthogonal Matrices - Examples with Solutions

Definition of Orthogonal Matrices

An n × n matrix whose columns form an orthonormal set is called an orthogonal matrix.
As a reminder, a set of vectors is orthonormal if each vector is a unit vector ( length or norm of the vector is equal to n × n and each vector in the set is orthogonal to all other vectors in the set.
These are examples of orthogonal matrices.

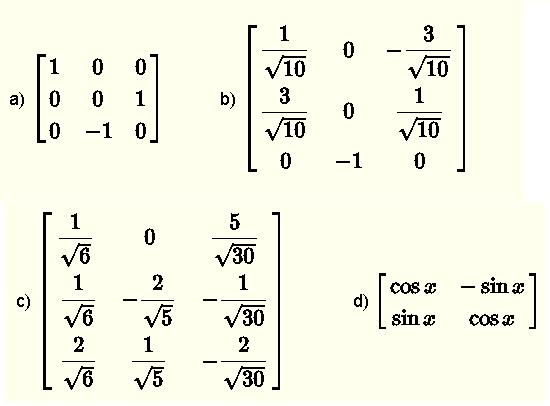
Properties of Orthogonal Matrices

A list of the most important properties of orthogonal matrices is given below. If Q is an orthogonal matrix, then

1.    Q^-1 = Q^T ; this is the most important property of orthogonal matrices as the inverse is simply the transpose.
2.   the rows of Q form an orthonormal set.
3.    Q^-1 is an orthogonal matrix
4.   Det( Q ) = ~+mn~ 1
5.   if λ is an eigrnvalue of ( Q ) , then | λ | = 1
6.   if Q₁ and Q₂ are n × n orthogonal matrices, then Q₁ Q₂ is also an orthogonal matrix.

Examples with Solutions

Example 1
The matrices \( Q_1 = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \) and \( Q_2 = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{bmatrix} \) are orthogonal. Verify that the product \( Q_1 Q_2 \) is also orthogonal (Property 6 above)

Solution
We first calculate the product \( Q_1 Q_2 \)
\( Q_1 Q_2 = \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{bmatrix} = \begin{bmatrix} 0&0&-1\\ 0&-1&0\\ 1&0&0 \end{bmatrix} \)

Let \( \textbf v_1 , \textbf v_2 , \textbf v_3 \) be the columns of the matrix \( Q_1 Q_2 \) found above.
\( \textbf {v}_1 = \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix} \) , \( \textbf {v}_2 = \begin{bmatrix} 0\\ -1\\ 0 \end{bmatrix} \) , \( \textbf {v}_3 = \begin{bmatrix} -1\\ 0\\ 0 \end{bmatrix} \)

Let us calculate the length or norm of each column
\( || \textbf {v}_1 || = \sqrt {0^2+0^2+1^2} = 1 \)
\( || \textbf {v}_2 || = \sqrt {0^2+(-1)^2+0^2} = 1 \)
\( || \textbf {v}_3 || = \sqrt {(-1)^2+0^2+0^2} = 1 \)

All three vectors are unit vectors.

Calculate the inner product of all pairs of vectors that can be made from the vectors \( \textbf v_1 , \textbf v_2 , \textbf v_3 \)
\( \textbf {v}_1 \cdot \textbf {v}_2 = 0 \cdot 0 + 0 \cdot (-1) + 1 \cdot 0 = 0 \)
\( \textbf {v}_1 \cdot \textbf {v}_3 = 0 \cdot (-1) + 0 \cdot 0 + 1 \cdot 0 = 0 \)
\( \textbf {v}_2 \cdot \textbf {v}_3 = 0 \cdot (-1) + (-1) \cdot 0 + 0 \cdot 0 = 0 \)
The three vectors form an orthogonal set.
The three columns of the matrix \( Q_1 Q_2 \) are orthogonal and have norm or length equal to 1 and are therefore orthonormal.

Example 2
Use a calculator to find the inverse of the orthogonal matrix \( Q = \begin{bmatrix} 0 & 0 & 1 \\ -1 & 0 & 0 \\ 0 & -1 & 0 \end{bmatrix} \) and verify Property 1 above.

Solution
Use any matrix calculator to find
\( Q^{-1} = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix} \)

Find the transpose of matrix \( Q \)
\( Q^T = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix} \)
Hence \( Q^{-1} = Q^T \) , property 1 above.

Example 3
Find the real constants \( a \) and \( b \) in the matrix \( Q = \begin{bmatrix} -1 & 0 & 0 \\ 0 & \dfrac{1}{\sqrt 2} & a \\ 0 & \dfrac{1}{\sqrt 2} & b \end{bmatrix} \) such that \( Q \) is orthogonal.

Solution
Let \( \textbf v_1 , \textbf v_2 , \textbf v_3 \) be the columns of the matrix \( Q \) given above such that
\( \textbf {v}_1 = \begin{bmatrix} -1\\ 0\\ 0 \end{bmatrix} \) , \( \textbf {v}_2 = \begin{bmatrix} 0\\ \dfrac{1}{\sqrt 2}\\ \dfrac{1}{\sqrt 2} \end{bmatrix} \) , \( \textbf {v}_3 = \begin{bmatrix} 0\\ a\\ b \end{bmatrix} \)

Two sets of conditions for matrix \( Q \) to be orthogonal:
1) The norm of each column \( \textbf v_1 , \textbf v_2 , \textbf v_3 \) must equal to 1
\( || \textbf v_1 || = \sqrt {(-1)^2+0^2+0^2} = 1 \)
\( || \textbf v_2 || = \sqrt {0^2+ \left(\dfrac{1}{\sqrt 2} \right)^2+\left(\dfrac{1}{\sqrt 2} \right)^2 } = 1 \)
\( || \textbf v_3 || = \sqrt {0^2+a^2+b^2} = \sqrt {a^2+b^2} = 1 \)         (I)

2) The inner product of any two vectors must be equal to zero (orthogonal vectors)
\( \textbf {v}_1 \cdot \textbf {v}_2 = (-1) \cdot 0 + 0 \cdot \left(\dfrac{1}{\sqrt 2} \right) + 0 \cdot \left(\dfrac{1}{\sqrt 2} \right) = 0 \)
\( \textbf {v}_1 \cdot \textbf {v}_3 = (-1) \cdot 0 + 0 \cdot a + 0 \cdot b = 0 \)
\( \textbf {v}_2 \cdot \textbf {v}_3 = 0 \cdot 0 + \dfrac{1}{\sqrt 2} \cdot a + \dfrac{1}{\sqrt 2} \cdot b = \dfrac{1}{\sqrt 2} \cdot a + \dfrac{1}{\sqrt 2} \cdot b = 0 \)         (II)

For all conditions to be satisfied, we need to solve equations (I) and (II) above
Equation (II) above gives \( a = - b \)

Substitute \( a \) by \( - b \) in equation (I) to obtain
\( \sqrt {2 b^2 } = 1 \)

Solve to obtain
\( b = \pm \dfrac{1}{\sqrt 2} \)

Two solutions to the above question
\( a = - \dfrac{1}{\sqrt 2} \) and \( b = \dfrac{1}{\sqrt 2} \)
\( a = \dfrac{1}{\sqrt 2} \) and \( b = - \dfrac{1}{\sqrt 2} \)

Questions (with solutions given below)

• Part 1
  Matrix \( Q = \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \) is orthogonal. Verify the first 5 properties, listed above, for matrix \( Q \).
  
• Part 2
  1) Which of the following matrices are orthogonal?
  a) \( A = \begin{bmatrix} \dfrac{1}{\sqrt 2} & \dfrac{1}{\sqrt 2} \\ - \dfrac{1}{\sqrt 2} & \dfrac{1}{\sqrt 2} \end{bmatrix} \) , b) \( B = \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix} \) , c) \( C = \begin{bmatrix} \dfrac{1}{\sqrt {10}} & - \dfrac{3}{\sqrt {10}} & 0 \\ 0 & 0 & 1 \\ \dfrac{3}{\sqrt {10}} & \dfrac{1}{\sqrt {10}} & 0 \end{bmatrix} \)
  
• Part 3
  1) Find all matrices of the form \( A = \begin{bmatrix} p & q\\ \dfrac{1}{\sqrt {3}} & r \end{bmatrix} \) that are orthogonal.
  
• Part 4
  Find the inverse of matrix \( A = \begin{bmatrix} 0 & \dfrac{5}{3 \sqrt 5} & \dfrac{2}{3} \\ \dfrac{1}{\sqrt 5} & - \dfrac{4}{3 \sqrt 5} & \dfrac{2}{3} \\ \dfrac{2}{\sqrt 5} & \dfrac{2}{3 \sqrt 5} & - \dfrac{1}{3} \end{bmatrix} \)
  

Solutions to the Above Questions

• Part 1
  Property 1
  Use a calculator to calculate \( Q^{-1} \)
  \( Q^{-1} = \begin{bmatrix}0&-1&0\\ 1&0&0\\ 0&0&1\end{bmatrix} \)
  Determine \( Q^T \)
  \( Q^T = \begin{bmatrix}0&-1&0\\ 1&0&0\\ 0&0&1\end{bmatrix} \)
  We conclude that \( Q^{-1} = Q^T \)
  Property 2
  The rows of \( Q \) may be represented by the vectors \( \textbf {v}_1 = \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix} \) , \( \textbf {v}_2 = \begin{bmatrix} -1\\ 0\\ 0 \end{bmatrix} \) , \( \textbf {v}_3 = \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix} \)
  Calculate the length or norm of each vector
  \( ||\textbf {v}_1 || = \sqrt {0^2+1^2+0^2} = 1 \)
  \( ||\textbf {v}_2 || = \sqrt {(-1)^2+0^2+0^2} = 1 \)
  \( ||\textbf {v}_3 || = \sqrt {0^2+0^2+1^2} = 1 \)
  Calculate the inner product of each pair of vectors
  \( \textbf {v}_1 \cdot \textbf {v}_2 = 0\cdot(-1) + 1\cdot0 + 0\cdot0 = 0 \)
  \( \textbf {v}_1 \cdot \textbf {v}_3 = 0\cdot0 + 1\cdot0 + 0\cdot1 = 0 \)
  \( \textbf {v}_2 \cdot \textbf {v}_3 = (-1)\cdot0 + 0\cdot0 + 0\cdot1 = 0 \)
  The rows of \( Q \) form an orthonormal set of vectors.
  Property 3
  We have already calculated \( Q^{-1} = \begin{bmatrix}0&-1&0\\ 1&0&0\\ 0&0&1\end{bmatrix} \)
  We can easily check that the column vectors of \( Q^{-1} \) are the same as the row vectors \( \textbf {v}_1 , \textbf {v}_2 , \textbf {v}_3 \) already shown above (in property 2) that they form an orthonormal set. Hence \( Q^{-1} \) is an orthogonal matrix.
  Property 4
  Using the first row of \( Q \), we calculate the determinant as follows
  Det \( (Q) = - 1 \cdot \text{Det} \begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix} = 1 \)
  Property 5
  Find the eigenvalues of \( Q \) by solving the equation
  \( \det \left\{ \:\begin{bmatrix}\:\:\:0\:\:&\:1\:&\:0\:\\ \:\:\:\:\:-1\:\:\:&\:0\:&\:0\:\\ \:\:\:\:\:0\:&\:0\:&\:1\end{bmatrix} - \lambda \:\begin{bmatrix}\:\:\:1\:\:&\:0\:&\:0\:\\ \:\:\:\:\:0\:\:\:&\:1\:&\:0\:\\ \:\:\:\:\:0\:&\:0\:&\:1\end{bmatrix} \right \} =0 \)
  Simplify the left side of the above and rewrite as
  \( \det \begin{bmatrix}-\lambda&1&0\\ -1&-\lambda&0\\ 0&0&1-\lambda\end{bmatrix} = 0 \)
  Use the third row (it has 2 zeros)) to evaluate the determinant on the left side of the equation
  \( (1 - \lambda) ( \lambda^2 + 1 ) = 0 \)
  Solve the above equation to find all eigenvalues
  \( \lambda_1 = 1 \) , \( \lambda_2 = i \) and \( \lambda_3 = - i \)
  and we can now conclude that
  \( |\lambda_1| = 1 \) , \( |\lambda_2| = 1 \) and \( |\lambda_3| = 1 \)
  
  
  
• Part 2
  Matrices A and C are orthogonal but matrix B is not because its columns 2 and 3 are not orthogonal.
  
  
• Part 3
  Two conditions must be satisfied for matrix \( A = \begin{bmatrix} p & q\\ \dfrac{1}{\sqrt {3}} & r \end{bmatrix} \) to be orthogonal.
  1) The vectors formed by the column must be unit vectors (norm equal to 1). Hence
  \( \sqrt {p^2 + \left(\dfrac{1}{\sqrt {3}}\right)^2} = 1 \)         (I)
  and
  \( \sqrt {q^2 + r^2 } = 1 \)         (II)
  Solve equation (I) to obtain two solutions
  \( p_1=\sqrt{\dfrac{2}{3}}\) and \( p_2=-\sqrt{\dfrac{2}{3}} \)
  2) The two columns must be orthogonal which gives the equation
  \( p q + \dfrac{r}{\sqrt {3}} = 0 \)         (III)
  
  Use the first solution \( p_1 \) to find \( q\) and \( r \)
  Let \( p = \sqrt{\dfrac{2}{3}} \) and substitute in equation (III)
  \( \sqrt{\dfrac{2}{3}} q + \dfrac{r}{\sqrt {3}} = 0 \)
  which gives
  \( q = - \dfrac{\sqrt{2}r}{2} \)         (IV)
  Substitute in equation (II) to obtain the equation
  \( \sqrt { \left(- \dfrac{\sqrt{2}r}{2}\right)^2 + r^2 } = 1 \)
  Solve the above to find
  \( r_1 =\sqrt{\dfrac{2}{3}} \) and \( r_2 = -\sqrt{\dfrac{2}{3}} \)
  Substitute in equation (IV) to obtain the corresponding values of \( q \)
  \( q_1 = -\dfrac{\sqrt{3}}{3} \) and \( q_2 = \dfrac{\sqrt{3}}{3} \)
  
  Use the second solution \( p_2 \) to find \( q\) and \( r \)
  Let \( p = - \sqrt{\dfrac{2}{3}} \) and substitute in equation (III)
  \( - \sqrt{\dfrac{2}{3}} q + \dfrac{r}{\sqrt {3}} = 0 \)
  which gives
  \( q = \dfrac{\sqrt{2}r}{2} \)         (V)
  Substitute in equation (II) to obtain the equation
  \( \sqrt {\left(\dfrac{\sqrt{2}r}{2}\right)^2 + r^2 } = 1 \)
  Solve the above to find
  \( r_3 =\sqrt{\dfrac{2}{3}} \) and \( r_4 = -\sqrt{\dfrac{2}{3}} \)
  Substitute in equation (IV) to obtain the corresponding values of \( q \)
  \( q_3 = \dfrac{\sqrt{3}}{3} \) and \( q_4 = -\dfrac{\sqrt{3}}{3} \)
  
  The matrices are
  \(\begin{bmatrix} \sqrt{\dfrac{2}{3}} & -\dfrac{\sqrt{3}}{3}\\ \dfrac{1}{\sqrt {3}} & \sqrt{\dfrac{2}{3}} \end{bmatrix} \) , \(\begin{bmatrix} \sqrt{\dfrac{2}{3}} & \dfrac{\sqrt{3}}{3}\\ \dfrac{1}{\sqrt {3}} & -\sqrt{\dfrac{2}{3}} \end{bmatrix} \) , \(\begin{bmatrix} - \sqrt{\dfrac{2}{3}} & \dfrac{\sqrt{3}}{3}\\ \dfrac{1}{\sqrt {3}} & \sqrt{\dfrac{2}{3}} \end{bmatrix} \) , \(\begin{bmatrix} - \sqrt{\dfrac{2}{3}} & -\dfrac{\sqrt{3}}{3}\\ \dfrac{1}{\sqrt {3}} & -\sqrt{\dfrac{2}{3}} \end{bmatrix} \) ,
  
  
• Part 4
  Given matrix \( A = \begin{bmatrix} 0 & \dfrac{5}{3 \sqrt 5} & \dfrac{2}{3} \\ \dfrac{1}{\sqrt 5} & - \dfrac{4}{3 \sqrt 5} & \dfrac{2}{3} \\ \dfrac{2}{\sqrt 5} & \dfrac{2}{3 \sqrt 5} & - \dfrac{1}{3} \end{bmatrix} \)
  Any of the known methods may be used to find the inverse of matrix \( A \). But a close examination of the matrix reveals that the matrix is orthogonal.
  Let us prove that the given matrix is orthogonal.
  Let \( \textbf v_1 , \textbf v_2 , \textbf v_3 \) be the columns of matrix \( A \) given above such that
  \( \textbf {v}_1 = \begin{bmatrix} 0\\ \dfrac{1}{\sqrt 5} \\ \dfrac{2}{\sqrt 5} \end{bmatrix} \) , \( \textbf {v}_2 = \begin{bmatrix} \dfrac{5}{3 \sqrt 5}\\ - \dfrac{4}{3 \sqrt 5}\\ \dfrac{2}{3 \sqrt 5} \end{bmatrix} \) , \( \textbf {v}_3 = \begin{bmatrix} \dfrac{2}{3}\\ \dfrac{2}{3}\\ -\dfrac{1}{3} \end{bmatrix} \)
  Let us calculate the length or norm of each vector.
  \( || \textbf {v}_1 || = \sqrt {0^2+ \left(\dfrac{1}{\sqrt 5} \right)^2+ \left(\dfrac{2}{\sqrt 5} \right)^2} = 1 \)
  \( || \textbf {v}_2 || = \sqrt { \left(\dfrac{5}{3 \sqrt 5}\right)^2+ \left(- \dfrac{4}{3 \sqrt 5} \right)^2+ \left(\dfrac{2}{3 \sqrt 5} \right)^2} = 1 \)
  \( || \textbf {v}_3 || = \sqrt { \left(\dfrac{2}{3} \right)^2+ \left(\dfrac{2}{3} \right)^2+ \left(-\dfrac{1}{3} \right)^2 } = 1 \)
  All three vectors formed by the columns of the given matrix are unit vectors (norm or length = 1)
  Calculate the inner product of all pairs of vectors that can be made from the vectors \( \textbf v_1 , \textbf v_2 , \textbf v_3 \)
  \( \textbf {v}_1 \cdot \textbf {v}_2 = 0 \cdot \left(\dfrac{5}{3 \sqrt 5}\right) + \left(\dfrac{1}{\sqrt 5} \right) \cdot \left(- \dfrac{4}{3 \sqrt 5} \right) + \left(\dfrac{2}{\sqrt 5} \right) \cdot \left(\dfrac{2}{3 \sqrt 5} \right) = 0 \)
  \( \textbf {v}_1 \cdot \textbf {v}_3 = 0 \cdot \left(\dfrac{2}{3}\right) + \left(\dfrac{1}{\sqrt 5} \right) \cdot \left(\dfrac{2}{3}\right) + \left(\dfrac{2}{\sqrt 5} \right) \cdot \left(-\dfrac{1}{3}\right) = 0 \)
  \( \textbf {v}_2 \cdot \textbf {v}_3 = \left(\dfrac{5}{3 \sqrt 5}\right) \cdot \left(\dfrac{2}{3}\right) + \left(- \dfrac{4}{3 \sqrt 5} \right) \cdot \left(\dfrac{2}{3}\right) + \left(\dfrac{2}{3 \sqrt 5} \right) \cdot \left(-\dfrac{1}{3}\right) = 0 \)
  The three vectors formed by the columns of the given matrix are orthogonal. Therefore the given matrix is orthogonal and we may the property \( A^{-1} = A^T \); hence the inverse of matrix \( A \) is given by the transpose of matrix \( A \).
  \( A^{-1} = \begin{bmatrix} 0 & \dfrac{1}{\sqrt 5} & \dfrac{2}{\sqrt 5} \\ \dfrac{5}{3 \sqrt 5} & - \dfrac{4}{3 \sqrt 5} & \dfrac{2}{3 \sqrt 5} \\ \dfrac{2}{3} & \dfrac{2}{3} & - \dfrac{1}{3} \end{bmatrix} \)
  

More References and links

• Matrices with Examples and Questions with Solutions.
  
• Determinant of a Square Matrix.
  
• Inverse Matrix Questions with Solutions.
  
• Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres
• Introduction to Linear Algebra - Fifth Edition (2016) - Gilbert Strang
• Linear Algebra Done Right - third edition, 2015 - Sheldon Axler
• Linear Algebra with Applications - 2012 - Gareth Williams