Linear Functions Problems with Solutions
Linear functions are highly used throughout mathematics and are therefore important to understand.
A set of problems involving linear functions, along with detailed solutions, are presented. The problems are designed with emphasis on the meaning of the slope and the y intercept.
Problem 1:
f is a linear function. Values of x and f(x) are given in the table below; complete the table.
f is a linear function whose formula has the form
f(x) = a x + b
where a and b are constants to be found. Note that 2 ordered pairs (-3,17) and (4,-18) are given in the table. These two ordered pairs are used to write a system of linear equations as follows
17 = - 3 a + b and -18 = 4 a + b
Solve the above system to obtain a = - 5 and b = 2 and write the formula for function f as follows
f(x) = - 5 x + 2
We now use the formula for f to find f(x) given x or find x given f(x).
for x = 0 , f(0) = -5(0) + 2 = 2
for f(x) = 1 , 1 = -5 x + 2 which gives x = 1 / 5
for x = 7 , f(7) = - 5(7) + 2 = - 33
for f(x) = - 30 , -30 = -5 x + 2 which gives x = 32 / 5
We now put the values calculated above in the table.
Problem 2:
A family of linear functions is given by
where x is the independent variable and m is a constant.
a) Graph f for m = 0, 1, 2, -3 and -5
b) What do all the graphs in part a) have in common?
c) Justify your answer to part b) analytically.
d) Write the equation of the family of functions whose graphs pass by the same point (- 2 , - 4).
Solution to Problem 2:
a)
b) All the graphs pass by the same point (2 , 3)
c) To prove that all lines described by the equation f(x) = mx + (3 - 2 m) pass by the point (2 , 3), show that f(2) = 3
f(2) = 2 m + (3 - 2m) = 3
d) The point slope form of the equation of a line is used to find equation of the family of lines that pass by the point (-2,-4) is found as follows
y - (-4) = m (x - (-2))
y = mx + (2m - 4)
As an exercise, graph the above equation for different values of m and check that all the lines obtained pass by the point (-2 , -4)
Problem 3:
A high school had 1200 students enrolled in 2003 and 1500 students in 2006. If the student population P ; grows as a linear function of time t, where t is the number of years after 2003.
a) How many students will be enrolled in the school in 2010?
b) Find a linear function that relates the student population to the time t.
Solution to Problem 3:
a) The given information may be written as ordered pairs (t , P). The year 2003 correspond to t = 0 and the year 2006 corresponds to t = 3, hence the 2 ordered pairs
(0, 1200) and (3, 1500)
Since the population grows linearly with the time t, we use the two ordered pairs to find the slope m of the graph of P as follows
m = (1500 - 1200) / (6 - 3) = 100 students / year
The slope m = 100 means that the students population grows by 100 students every year. From 2003 to 2010 there are 7 years and the students population in 2010 will be
P(2010) = P(2003) + 7 * 100 = 1200 + 700 = 1900 students.
b) We know the slope and two points, we may use the point slope form to find an equation for the population P as a function of t as follows
P - P1 = m (t - t1)
P - 1200 = 100 (t - 0)
P = 100 t + 1200
Problem 4:
The graph shown below is that of the linear function that relates the value V (in $) of a car to its age t, where t is the number of years after 2000.
.
b) What will be the value of the car in the year 2010?
Solution to Problem 4: a) Find two points from the graph
(0 , 16000) and (7 , 7600)
Use the above points to find the slope m
m = (7600 - 16000) / (7 - 0) = - 1200 $ / year
A slope of - 1200 $ / year means that the value of the car decreases by 1200 $ every year.
b) In 2010, t = 10. There are 3 years from t = 7 to t = 10. The value of the car will be given by
7600 - 3 * 1200 = $4000
Problem 5:
The cost of producing x tools by a company is given by
a) What is the cost of 100 tools?
b) What is the cost of 101 tools?
c) Find the difference between the cost of 101 and 100 tools.
d) Find the slope of the graph of C?
e) Interpret the slope.
Solution to Problem 5:
a)
C(100) = 1200*100 + 5500 = $125500
b)
C(101) = 1200*101 + 5500 = $126700
c)
C(101)-C(100) = $1200
d) Slope m is given by
m = 1200 $ / (1 tool)
e) Slope is the increase in the total cost C when the number of tools produced increases by 1 unit.
Problem 6:
A 500-liter tank full of oil is being drained at the constant rate of 20 liters par minute.
a) Write a linear function V for the number of liters in the tank after t minutes (assuming that the drainage started at t = 0).
b) Find the V and the t intercepts and interpret them.
e) How many liters are in the tank after 11 minutes and 45 seconds?
Solution to Problem 6:
After each minute the amount of oil in the tank deceases by 20 liters. After t minutes, the amount of oil in the tank decreases by 20*t liters. Hence if at the start there 500 liters, after t minute the amount V of oil left in the tank is given by
V = 500 - 20 t
b) To find the V intercept, set t = 0 in the equation V = 500 - 20 t.
V = 500 liters : it is the amount of oil at the start of the drainage.
To find the t intercept, set V = 0 in the equation V = 500 - 20 t and solve for t.
0 = 500 - 20 t
t = 500 / 20 = 25 minutes : it is the total time it takes to drain the 500 liters of oil.
c) Convert 11 minutes 45 seconds in decimal form.
t = 11 minutes 45 seconds = 11.75 minutes
Calculate V at t = 11.75 minutes.
V(11.75) = 500 - 20*11.75 = 265 liters are in the tank after 11 minutes 45 seconds of drainage.
Problem 7:
A 50-meter by 70-meter rectangular garden is surrounded by a walkway of constant width x meters.
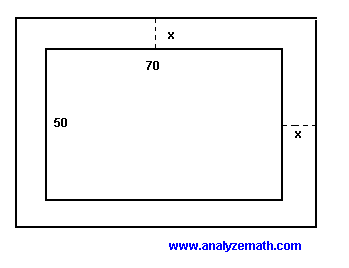
a) Write the outside perimeter P in terms of x.
b) Find the slope of the graph of P.
c) What is the meaning of the slope found in b)?
Solution to Problem 7:
a) Perimeter P is given by
P = 2 Lengths + 2 widths = 2(70 + 2x) + 2(50 + 2x) = 8 x + 240
b) The slope of P is equal to 8.
c)Whenever x increases by 1 meter, the outside perimeter increases by 8 meters.
Problem 8:
A driver starts a journey with 25 gallons in the tank of his car. The car burns 5 gallons for every 100 miles. Assuming that the amount of gasoline in the tank decreases linearly,
a) write a linear function that relates the number of gallons G left in the tank after a journey of x miles.
b) What is the value and meaning of the slope of the graph of G?
c) What is the value and meaning of the x intercept?
Solution to Problem 8:
a) If 5 gallons are burnt for 100 miles then (5 / 100) gallons are burnt for 1 mile. Hence for x miles, x * (5 / 100) gallons are burnt. G is then equal to the initial amount of gasoline decreased by the amount gasoline burnt by the car. Hence
G = 25 - (5 / 100) x
b) The slope of G is equal to 5 / 1000 and it represent the amount of gasoline burnt for a distance of 1 mile.
c) To find the x intercept, we set G = 0 and solve for x.
25 - (5 / 100) x = 0
x = 500 miles : it is the distance x for which all 25 gallons of gasoline will be burnt.
Problem 9:
A rectangular wire frame has one of its dimensions moving at the rate of 0.5 cm / second. Its width is constant and equal to 4 cm. If at t = 0 the length of the rectangle is 10 cm,
a) what is the length at time t.
b) Write a formula for the area A of the rectangle in terms of t.
c) Write a formula for the perimeter P of the rectangle in terms of t.
c) As x increases, which one, the perimeter or the area, increases faster?
Solution to Problem 9:
a) Length x at t
x = 10 + 0.5 * t , t in seconds
b) Area A is given by
A = width * length = 4 (10 + 0.5 t) = 2 t + 40 cm 2 .
c) Perimeter P is given by
P = 2 widths + 2 Lengths = 2*4 + 2*(10 + 0.5 t) = t + 28 cm
c) The area increases faster since its slope is larger than that of the perimeter. More math problems with detailed solutions in this site.
