Parabola and Line Intersection Problem

Q: How do you find the equation of a parabola given its vertex and one point?

Use the vertex form y = a(x - h)² + k, where (h, k) is the vertex. Substitute the coordinates of the known point into the equation to solve for a. For example, with vertex (4, -4) and point (2, 0), 0 = a(2-4)² - 4 gives a = 1.

Q: How do you solve the inequality f(x) > g(x) graphically?

Identify the x-values where the graph of f(x) lies above the graph of g(x). For a parabola opening upward intersected by a line at x = 2 and x = 7, the parabola is above the line for x 7, so the solution is (-∞, 2) ∪ (7, +∞).

Q: What is the vertex form of a parabola?

The vertex form of a parabola is y = a(x - h)² + k, where (h, k) is the vertex. The parameter a determines the direction and width of the parabola: if a > 0, it opens upward; if a < 0, it opens downward.

Q: How do you determine whether a parabola opens upward or downward?

The sign of the leading coefficient a determines the direction. If a > 0, the parabola opens upward (concave up). If a < 0, the parabola opens downward (concave down). In this problem, a = 1, so the parabola opens upward.

In this algebra problem, we explore the intersection of a parabola and a line using their graphs. Problems like this are common in Algebra and Pre-Calculus, since they combine concepts of quadratic functions, linear functions, and inequalities.

Table of Contents

Problem Statement

The graphs of a parabola given by \( y = f(x) \) and a line given by \( y = g(x) \) are shown below. The parabola and the line intersect at points \( A \) and \( D \); where \( A \) is on the x-axis and has an x-coordinate equal to \( 2 \). Point \( V \) is the vertex of the parabola.

Based on the provided graph coordinates, the line also passes through \( C(-3, -5) \), and the vertex is at \( V(4, -4) \).

Graph of a parabola and a line intersecting at points A(2,0) and D, with vertex V(4,-4) and point C(-3,-5) on the line

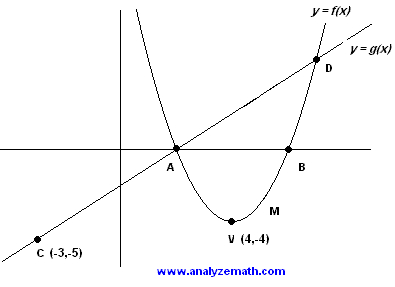Find the equation of the line \( g \) and write it in the form \( g(x) = mx + b \).
Find the equation of the parabola \( f(x) \).
Find the x-coordinate of point \( D \).
Use the graph and the equations to solve the inequality \( f(x) \gt g(x) \).

Step-by-Step Solution

View Full Solution

Part (a): Equation of the line \( g \)

The line \( y = g(x) \) passes through the points \( C(-3, -5) \) and \( A(2, 0) \).

First, calculate the slope \( m \):

\[ m = \frac{0 - (-5)}{2 - (-3)} = \frac{5}{5} = 1 \]

Next, use the point-slope form of the equation of a line:

\[ y - 0 = 1(x - 2) \]

Which simplifies to:

\[ y = x - 2 \]

Hence, the equation of the line is:

\[ \boxed{g(x) = x - 2} \]

Part (b): Equation of the parabola \( f \)

The vertex of the parabola is known to be \( V(4, -4) \). The equation of the parabola in vertex form is given by:

\[ y = a(x - h)^2 + k \implies y = a(x - 4)^2 - 4 \]

Point \( A(2, 0) \) is on the parabola. Substitute \( x = 2 \) and \( y = 0 \) into the equation to find \( a \):

\[ 0 = a(2 - 4)^2 - 4 \] \[ 0 = a(-2)^2 - 4 \] \[ 0 = 4a - 4 \implies 4a = 4 \implies a = 1 \]

Hence, the equation of the parabola is given by:

\[ \boxed{f(x) = (x - 4)^2 - 4} \]

Note: Expanding this gives \( f(x) = x^2 - 8x + 12 \).

Part (c): The x-coordinate of point \( D \)

The points of intersection are determined by setting \( f(x) \) equal to \( g(x) \):

\[ (x - 4)^2 - 4 = x - 2 \]

Expand and simplify the equation:

\[ x^2 - 8x + 16 - 4 = x - 2 \] \[ x^2 - 8x + 12 = x - 2 \] \[ x^2 - 9x + 14 = 0 \]

Factor the quadratic equation:

\[ (x - 2)(x - 7) = 0 \]

This yields the solutions \( x = 2 \) and \( x = 7 \).

Since \( x = 2 \) is already known to be the x-coordinate of point \( A \), it follows that \( x = 7 \) is the x-coordinate of point \( D \).

\[ \boxed{D = (7, \; 5)} \]

Note: The y-coordinate of \( D \) is found by \( g(7) = 7 - 2 = 5 \).

Part (d): Solving the inequality \( f(x) \gt g(x) \)

Geometrically, \( f(x) \gt g(x) \) in the regions where the parabola is above the line.

From the left side of the graph up to point \( A \) (where \( x = 2 \)), the parabola is above the line, so the interval \( (-\infty, 2) \) is part of the solution set.
Similarly, from point \( D \) (where \( x = 7 \)) to the right side of the graph, the parabola is again above the line, providing the interval \( (7, +\infty) \).

Therefore, the complete solution set for the inequality \( f(x) \gt g(x) \) is given by the union of these intervals:

\[ \boxed{(-\infty, 2) \cup (7, +\infty)} \]

Verification of the Solution

Check 1 — Both intersection points satisfy both equations:

At \( x = 2 \): \( f(2) = (2-4)^2 - 4 = 4 - 4 = 0 \); \( g(2) = 2 - 2 = 0 \). ✓
At \( x = 7 \): \( f(7) = (7-4)^2 - 4 = 9 - 4 = 5 \); \( g(7) = 7 - 2 = 5 \). ✓

Check 2 — The vertex \( V(4, -4) \) is indeed on the parabola:

\( f(4) = (4-4)^2 - 4 = 0 - 4 = -4 \). ✓

Check 3 — The inequality holds in a sample test point:

Take \( x = 0 \) (which is in the interval \( (-\infty, 2) \)):

\( f(0) = (0-4)^2 - 4 = 16 - 4 = 12 \) and \( g(0) = 0 - 2 = -2 \). Since \( 12 \gt -2 \), the inequality holds. ✓

Take \( x = 5 \) (which is between 2 and 7, so should NOT be a solution):

\( f(5) = (5-4)^2 - 4 = 1 - 4 = -3 \) and \( g(5) = 5 - 2 = 3 \). Since \( -3 \lt 3 \), the inequality does NOT hold. ✓

Summary of Results

Item	Result
Line equation \( g(x) \)	\( g(x) = x - 2 \)
Parabola equation \( f(x) \)	\( f(x) = (x-4)^2 - 4 = x^2 - 8x + 12 \)
Vertex of parabola	\( V(4, -4) \)
Intersection point A	\( A(2, 0) \)
Intersection point D	\( D(7, 5) \)
Solution to \( f(x) \gt g(x) \)	\( (-\infty, 2) \cup (7, +\infty) \)

Key Concepts Reviewed

Skills Practiced in This Problem

Slope of a line: \( m = \frac{y_2 - y_1}{x_2 - x_1} \) — used to find the slope of the line through two points.
Point-slope form: \( y - y_1 = m(x - x_1) \) — used to write the equation of the line.
Vertex form of a parabola: \( y = a(x-h)^2 + k \) — used to write the parabola equation given its vertex.
Solving for a parameter: Substituting a known point into the vertex form to find \( a \).
Solving systems of equations: Setting \( f(x) = g(x) \) and solving the resulting quadratic.
Factoring quadratics: \( x^2 - 9x + 14 = (x-2)(x-7) \).
Quadratic inequalities: Reading the solution from the graph and verifying algebraically.
Interval notation: \( (-\infty, 2) \cup (7, +\infty) \).

Frequently Asked Questions

How do you find the equation of a parabola given its vertex and one point?

Use the vertex form \( y = a(x - h)^2 + k \), where \( (h, k) \) is the vertex. Substitute the coordinates of the known point into the equation to solve for \( a \). For example, with vertex \( (4, -4) \) and point \( (2, 0) \), \( 0 = a(2-4)^2 - 4 \) gives \( a = 1 \).

How do you find the intersection points of a parabola and a line?

Set the equation of the parabola equal to the equation of the line, then solve the resulting quadratic equation. For example, \( (x-4)^2 - 4 = x - 2 \) simplifies to \( x^2 - 9x + 14 = 0 \), which factors as \( (x-2)(x-7) = 0 \), giving intersection x-coordinates 2 and 7.

How do you solve the inequality \( f(x) \gt g(x) \) graphically?

Identify the x-values where the graph of \( f(x) \) lies above the graph of \( g(x) \). For a parabola opening upward intersected by a line at \( x = 2 \) and \( x = 7 \), the parabola is above the line for \( x \lt 2 \) and \( x \gt 7 \), so the solution is \( (-\infty, 2) \cup (7, +\infty) \).

What is the vertex form of a parabola?

The vertex form of a parabola is \( y = a(x - h)^2 + k \), where \( (h, k) \) is the vertex. The parameter \( a \) determines the direction and width of the parabola: if \( a \gt 0 \), it opens upward; if \( a \lt 0 \), it opens downward.

How do you determine whether a parabola opens upward or downward?

The sign of the leading coefficient \( a \) determines the direction. If \( a \gt 0 \), the parabola opens upward (concave up). If \( a \lt 0 \), the parabola opens downward (concave down). In this problem, \( a = 1 \), so the parabola opens upward.