Rate, Time, and Distance Problems – Solved Examples with Step-by-Step Solutions

The relationship between distance, rate (speed), and time, $Distance = Time \times Rate,$ is the foundation for solving uniform motion problems in mathematics. In this guide, you will find **step-by-step solutions**, worked examples, and clear explanations to help you master rate, time, and distance problems.

Question 1 - Two cars traveling in opposite directions

Two cars started from the same point, at 5 am, traveling in opposite directions at $40 mph$ and $50 mph$ respectively. At what time will they be $450 miles$ apart?

Solution:

After $t$ hours, the distances $D_{1}$ and $D_{2}$ , in miles per hour, travelled by the two cars are given by $D_{1} = 40 t and D_{2} = 50 t$ After $t$ hours, the distance $D$ separating the two cars is given by $D = D_{1} + D_{2} = 40 t + 50 t = 90 t$ The distance $D$ will be equal to 450 miles when $D = 90 t = 450$ To find the time $t$ for $D$ to be 450 miles, solve the above equation for $t$ to obtain $t = 5 hours.$ Therefore, if the cars start at 5 am, they will be 450 miles apart at $5 am + 5 hours = 10 am.$

Question 2 - Car B passing Car A

At 9 am, a car $A$ began a journey from a point, traveling at 40 mph. At 10 am, another car $B$ started traveling from the same point at 60 mph in the same direction as car $A$ . At what time will car $B$ pass car $A$ ?

Solution:

After $t$ hours, the distance $D_{1}$ traveled by car A is given by $D_{1} = 40 t$ Car B starts at 10 am and will therefore have spent one hour less than car A when it passes it. After $(t - 1)$ hours, the distance $D_{2}$ traveled by car B is given by $D_{2} = 60 (t - 1)$ When car B passes car A, they are at the same distance from the starting point, and therefore $D_{1} = D_{2}$ , which gives $40 t = 60 (t - 1)$ Solving the above equation for $t$ gives $t = 3 hours$ Car B passes car A at $9 + 3 = 12 pm$

Question 3 - Two trains traveling towards each other

Two trains, traveling towards each other, left from two stations that are 900 miles apart, at 4 pm. If the rate of the first train is $72 mph$ and the rate of the second train is $78 mph$ , at what time will they pass each other?

Solution:

After $t$ hours, the two trains will have traveled distances $D_{1}$ and $D_{2}$ (in miles) given by $D_{1} = 72 t and D_{2} = 78 t$ After $t$ hours, the total distance $D$ traveled by the two trains is given by $D = D_{1} + D_{2} = 72 t + 78 t = 150 t$ When the distance $D$ is equal to 900 miles, the two trains pass each other: $150 t = 900$ Solve the above equation for $t$ : $t = 6 hours.$

Question 4 - Total distance driven by John

John left home and drove at the rate of $45 mph$ for $2$ hours. He stopped for lunch, then drove for another $3$ hours at the rate of $55 mph$ to reach his destination. How many miles did John drive?

Solution:

The total distance $D$ traveled by John is given by $D = 45 \times 2 + 3 \times 55 = 255 miles .$

Question 5 - Linda's driving rate before lunch

Linda left home and drove for 2 hours. She stopped for lunch, then drove for another 3 hours at a rate that is 10 mph higher than the rate before she had lunch. If the total distance Linda traveled is 230 miles, what was the rate before lunch?

Solution:

If $x$ is the rate at which Linda drove before lunch, the rate after lunch is equal to $x + 10$ . The total distance $D$ traveled by Linda is given by $D = 2 x + 3 (x + 10)$ and is equal to 230 miles. Hence $2 x + 3 (x + 10) = 230$ Solving for $x$ gives $x = 40 miles/hour .$

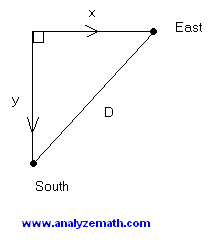
Question 6 - Two cars at right angles

Two cars leave, at 8 a.m., from the same point. One travels east at 50 mph and the other travels south at 60 mph. At what time will they be 300 miles apart?

Solution:

The two cars are traveling in directions that are at right angles. Let

x

and

y

be the distances traveled by the two cars in

t

hours. Hence:

x = 50 t and y = 60 t

Since the two directions are at right angles, Pythagoras' theorem can be used to find the distance

D

between the two cars as follows:

D = \sqrt{x^{2} + y^{2}}

We now find the time at which

D = 300

miles by solving:

\sqrt{x^{2} + y^{2}} = 300

Square both sides and substitute

x

and

y

50 t

and

60 t

respectively to obtain the equation:

(50 t)^{2} + (60 t)^{2} = 300^{2}

Solve the above equation to obtain:

t = 3.84 hours (rounded to two decimal places) or 3 hours and 51 minutes (to the nearest minute)

The two cars will be 300 miles apart at:

8 + 3 h 51^{'} = 11 : 51 am

Question 7 - Distance between two cities

By car, John traveled from city $A$ to city $B$ in 3 hours. At a rate that was 20 mph higher than John's, Peter traveled the same distance in 2 hours. Find the distance between the two cities.

Solution:

Let $x$ be John's rate in traveling between the two cities. The rate of Peter will be $x + 20$ . We use the rate-time-distance formula to write the distance $D$ traveled by John and Peter (same distance $D$ ): $D = 3 x and D = 2 (x + 20)$ The first equation can be solved for $x$ to give: $x = \frac{D}{3}$ Substitute $x$ by $\frac{D}{3}$ into the second equation: $D = 2 (\frac{D}{3} + 20)$ Solve for $D$ to obtain: $D = 120 miles$

Question 8 - Two cars crossing each other

Gary started driving at 9:00 am from city $A$ towards city $B$ at a rate of $50 mph$ . At a rate that is $15 mph$ higher than Gary's, Thomas started driving at the same time as John from city $B$ towards city $A$ through the same route. If Gary and Thomas crossed each other at 11:00 am, what is the distance between the two cities?

Solution:

Let $D$ be the distance between the two cities. When Gary and Thomas cross each other, they have covered all the distance between the two cities. Hence $D_{1} = 2 \times 50 = 100 miles, distance traveled by Gary$ $D_{2} = 2 \times (50 + 15) = 130 miles, distance traveled by Thomas$ The distance $D$ between the two cities is given by $D = D_{1} + D_{2} = 100 miles + 130 miles = 230 miles .$

Question 9 - Distance between two cars

Two cars started at the same time from the same point, driving along the same road. The speed of the first car is $50 mph$ and the speed of the second car is $60 mph$ . How long will it take for the distance between the two cars to be $30 miles$ ?

Solution:

Let $D_{1}$ and $D_{2}$ be the distances traveled by the two cars in $t$ hours. $D_{1} = 50 t and D_{2} = 60 t$ The second car has a higher speed, so the distance $d$ between the two cars is given by $d = 60 t - 50 t = 10 t$ For $d$ to be 30 miles, we have $30 = 10 t$ Solving the above equation for $t$ gives $t = 3 hours$

Question 10 - Two trains traveling in opposite directions

Two trains started at 10 PM from the same point. The first train traveled north at a speed of $80 mph$ and the second train traveled south at a speed of $100 mph$ . At what time were they $450$ miles apart?

Solution:

Let $D_{1}$ and $D_{2}$ be the distances traveled by the two trains in $t$ hours. $D_{1} = 80 t and D_{2} = 100 t$ Since the two trains are traveling in opposite directions, the total distance $D$ between the two trains is given by $D = D_{1} + D_{2} = 180 t$ For this distance to be 450 miles, we have $180 t = 450$ Solving for $t$ gives $t = 2.5 hours = 2 hours 30 minutes$ Thus, if the first train leaves at 10:00 pm, the trains will be 450 miles apart at $10 : 00 pm + 2 : 30 = 12 : 30 am .$

Question 11 - Two trains with one-hour delay

Two trains started from the same point. At 8:00 am, the first train traveled East at the rate of $80 mph$ . At 9:00 am, the second train traveled West at the rate of $100 mph$ . At what time were they $530$ apart?

Solution:

When the first train has traveled for $t$ hours, the second train will have traveled $(t - 1)$ hours since it started 1 hour late. Hence, if $D_{1}$ and $D_{2}$ are the distances traveled by the two trains, then $D_{1} = 80 t and D_{2} = 100 (t - 1)$ Since the trains are traveling in opposite directions, the total distance $D$ between the two trains is given by $D = D_{1} + D_{2} = 180 t - 100$ For $D$ to be 530 miles, we need to have $180 t - 100 = 530$ Solving for $t$ gives $t = 3 hours 30 minutes$ Adding this to the start time: $8 : 00 am + 3 : 30 = 11 : 30 am$