 .
.
How to solve questions on proportions in maths? Grade 7 maths questions are presented along with detailed solutions. Detailed Solutions and explanations are included.
What are proportions in maths and where are they needed?
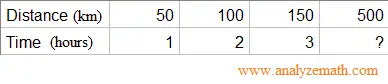
Example 1: The table below shows the distance travelled by a car in kilometers (km) and the time in hours necessary to travel that distance. We assume that the car travels at a constant speed. How many hours are needed to travel 500 kilometers?
 .
.
Solution
Note that if we divide the distance by time for the first three position, we obtain
50 / 1 = 50 , 100 / 2 = 50 , 150 / 3 = 50
The rates distance / time is constant and equal to 50 km/hour. We say that the distance is proportional to the distance and we can write: Distance = constant × time. In this example constant = 50.
Since the car is travelling at the same speed, we can say that this proportionality rule works also for the distance of 500 km and write
50 / 1 = 100 / 2 = 150 / 3 = 500 / t = 50
from the above we can write what we call a proportion:
150 / 3 = 500 / t
The difficulty in solving proportions is the presence of denominators such as 3 and t in this example. The main idea in solving proprotions is to eliminate the denominators. Before we proceed to solve the proportion above, let use look at the following mutliplication of the fraction 2 / 5 by its denominator 5 and see how the denominator is eliminated.
 .
.
 .
.
 .
.
 .
.
Solve the following proportions.
More Middle School Maths (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
More High School Maths (Grades 10, 11 and 12) - Free Questions and Problems With Answers
More Primary Maths (Grades 4 and 5) with Free Questions and Problems With Answers
Home Page