Math Problems with Solutions for Grade 8

We first convert the time of 4 hours 41 minutes into hours: \[ 4\ \text{hours} + 41\ \text{minutes} = 4 + \dfrac{41}{60} = \dfrac{240 + 41}{60} = \dfrac{281}{60}\ \text{hours} \] Average speed \( S \) is given by: \[ S = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{281\ \text{miles}}{\dfrac{281}{60}\ \text{hours}} = 281 \times \dfrac{60}{281} = 60\ \text{miles per hour} \] The average speed of the car is \( 60 \) miles per hour.

\[ 5x - 7 = 3x + 9 \] Subtract \( 3x \) from both sides: \[ 2x - 7 = 9 \] Add 7 to both sides: \[ 2x = 16 \] Divide both sides by 2: \[ x = 8 \]

We can solve this system using substitution.

From the second equation \( 4x - y = 7 \), solve for \( y \): \[ y = 4x - 7 \] Substitute \( y = 4x - 7 \) into the first equation: \[ 2x + 3(4x - 7) = 12 \] \[ 2x + 12x - 21 = 12 \] \[ 14x - 21 = 12 \] Add 21 to both sides: \[ 14x = 33 \] Now divide by 14: \[ x = \dfrac{33}{14} \] Substitute \( x = \dfrac{33}{14} \) into \( y = 4x - 7 \) to find \( y \): \[ y = 4\left(\dfrac{33}{14}\right) - 7 = \dfrac{132}{14} - 7 \] \[ = \dfrac{132}{14} - \dfrac{98}{14} = \dfrac{34}{14} = \dfrac{17}{7} \] The solution is \( x = \dfrac{33}{14} \) and \( y = \dfrac{17}{7} \).

First, simplify each square root. \[ \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \] \[ \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \] Now add the two simplified terms: \[ 5\sqrt{2} + 3\sqrt{2} = (5 + 3)\sqrt{2} = 8\sqrt{2} \] The simplified expression is \( 8\sqrt{2} \).

The formula for the area of a trapezoid is: \[ A = \dfrac{1}{2} \times (b_1 + b_2) \times h \] where \( b_1 \) and \( b_2 \) are the lengths of the parallel sides, and \( h \) is the height. Substitute the given values: \[ A = \dfrac{1}{2} \times (10 + 14) \times 6 \] \[ = \dfrac{1}{2} \times 24 \times 6 = 12 \times 6 = 72\ \text{cm}^2 \] The area of the trapezoid is \( 72\ \text{cm}^2 \).

Let \( L \) be the length and \( W \) be the width of the rectangle. Hence, \[ L = 4W \] We now use the area formula to write: \[ \text{Area} = L \times W \] Substitute \( L = 4W \) into the equation: \[ 100 = 4W \times W = 4W^2 \] Now, solve for \( W \): \[ 4W^2 = 100 \] \[ W^2 = 25 \] \[ W = 5 \] Since \( L = 4W \), the length is: \[ L = 4 \times 5 = 20 \ \text{m} \] The length of the rectangle is 20 meters.

Let \( L \) and \( W \) be the original length and width of the rectangle, and its area is given by: \[ A_{\text{original}} = L \times W \] After the increase, the length becomes \( 2L \) and the width becomes \( 3W \). The area of the new rectangle is then: \[ A_{\text{new}} = (2L) \times (3W) = 1800 \] Simplifying the equation: \[ 6L \times W = 1800 \] Now, solve for \( L \times W \): \[ L \times W = \dfrac{1800}{6} = 300 \, \text{square meters} \] Thus, the area of the original rectangle is \( 300 \) square meters.

Let \( x \) be the length of the edge of the original cube. When increased to twice its original size, the new edge length becomes \( 2x \), giving a volume of: \[ 2x \times 2x \times 2x = 8x^3 \] The volume is known to be 64,000 cubic centimeters. Hence, \[ 8x^3 = 64,000 \] Solving for \( x^3 \): \[ x^3 = \dfrac{64,000}{8} = 8,000 \] Taking the cube root of both sides: \[ x = \sqrt[3]{8,000} = 20 \] The area of one face of the original cube is given by: \[ x^2 = 20^2 = 400 \, \text{square centimeters} \] The area of one face of the original cube is \( 400 \) square centimeters.

In 1 hour, Pump A can fill \( \dfrac{1}{5} \) of a tank, and Pump B can fill \( \dfrac{1}{8} \) of the same tank. So, in 1 hour, the two pumps working together can fill: \[ \dfrac{1}{5} + \dfrac{1}{8} = \dfrac{13}{40} \text{ of a tank} \] Since the rate of the two pumps working together is \( \dfrac{13}{40} \), the time \( t \) needed to fill the tank by the two pumps is found by solving: \[ \left( \dfrac{13}{40} \right) t = 1 \] Solving for \( t \): \[ t = \dfrac{40}{13} = 3 \dfrac{1}{13} \text{ hours} \] This is equivalent to: \[ 3 \text{ hours and } \left( \dfrac{1}{13} \times 60 \right) \text{ minutes} = 3 \text{ hours and } 5 \text{ minutes} \quad (\text{rounded to the nearest minute}) \] It will take approximately 3 hours 5 minutes for the two pumps working together to fill the tank.

When water is pumped into a tank, the height of the water will increase. The graph in the top right side shows a decreasing height and the graph at the bottom right shows a constant height and cannot therefore represent the height as a function of time. The graph at the top left is not the graph of a function. The only graph that may represent the height of the water in the tank being filled is the graph in the bottom left which shows an increasing height.

Let the right triangle have legs \( a \), \( b \), and hypotenuse \( c \). We know:

One leg is \( a = 18 \) cm,

The area of the triangle is \( 216 \) square cm.

The area of a right triangle is given by: \[ \text{Area} = \dfrac{1}{2} \times \text{base} \times \text{height} \] Substituting the known values: \[ 216 = \dfrac{1}{2} \times 18 \times b \] Solving for \( b \): \[ 216 = 9b \] \[ b = \dfrac{216}{9} = 24 \, \text{cm} \] Now, we can use the Pythagorean theorem to find the hypotenuse \( c \): \[ c^2 = a^2 + b^2 \] \[ c^2 = 18^2 + 24^2 = 324 + 576 = 900 \] \[ c = \sqrt{900} = 30 \, \text{cm} \] Finally, the perimeter \( P \) of the triangle is the sum of the lengths of its sides: \[ P = a + b + c = 18 + 24 + 30 = 72 \, \text{cm} \] The perimeter of the triangle is \( 72 \, \text{cm} \).

To find the sum of the interior angles of a polygon with \( n \) sides, we use the formula: \[ \text{Sum of interior angles} = 180(n - 2) \] where \( n \) is the number of sides of the polygon. For a polygon with 53 sides (\( n = 53 \)): \[ \text{Sum of interior angles} = 180(53 - 2) = 180 \times 51 = 9180^\circ \] The sum of the interior angles of a polygon with 53 sides is \( 9180^\circ \).

We can represent the relative heights of the individuals based on the given information:

Jack is taller than Sarah but shorter than Malika and Tania*, which means: \[ \text{Sarah} < \text{Jack} < \text{Malika}, \quad \text{Jack} < \text{Tania} \] Malika is shorter than Tania, so: \[ \text{Malika} < \text{Tania} \] Natasha is shorter than Sarah, meaning: \[ \text{Natasha} < \text{Sarah} \] Thus, we can arrange the individuals in order of their height from shortest to tallest: \[ \text{Natasha} < \text{Sarah} < \text{Jack} < \text{Malika} < \text{Tania} \] The shortest person is Natasha.

Let the length of each leg of the isosceles right triangle be \( x \). Since it is an isosceles right triangle, both legs are equal in length. The area of a right triangle is given by: \[ \text{Area} = \dfrac{1}{2} \times \text{base} \times \text{height} \] In this case, both the base and the height are equal to \( x \), so the area becomes: \[ 800 = \dfrac{1}{2} \times x \times x \] Simplify the equation: \[ 800 = \dfrac{1}{2} \times x^2 \] Multiply both sides by 2 to eliminate the fraction: \[ 1600 = x^2 \] Now, solve for \( x \): \[ x = \sqrt{1600} = 40 \] So, the length of each leg is \( 40 \) feet. The hypotenuse \( h \) of a right triangle can be found using the Pythagorean theorem: \[ h^2 = x^2 + x^2 \] Since both legs are equal, this simplifies to: \[ h^2 = 2x^2 \] Substitute \( x = 40 \): \[ h^2 = 2 \times 40^2 = 2 \times 1600 = 3200 \] Now, take the square root of both sides: \[ h = \sqrt{3200} = 40\sqrt{2} \approx 56.57 \text{ feet} \] The height (one of the legs) of the isosceles right triangle is \( 40 \) feet, and the hypotenuse is approximately \( 40\sqrt{2} \) feet or \( 56.57 \) feet.

The circle is inscribed inside the square, meaning the diameter of the circle is equal to the side length of the square. Let the side length of the square be \( s = 20 \) meters. Thus, the diameter \( d \) of the circle is: \[ d = s = 20 \text{ meters} \] The radius \( r \) of the circle is half of the diameter: \[ r = \dfrac{d}{2} = \dfrac{20}{2} = 10 \text{ meters} \] The formula for the circumference \( C \) of a circle is: \[ C = 2\pi r \] Substituting the value of \( r \): \[ C = 2\pi \times 10 = 20\pi \text{ meters} \] Using \( \pi \approx 3.14 \): \[ C \approx 20 \times 3.14 = 62.8 \text{ meters} \] The circumference of the circle is approximately 62.8 meters.

Let \( x \) be the number of boys in school B. Hence, the number of boys in school A be \( 2x \) (since the ratio of boys in school A to boys in school B is 2:1).

Let the number of girls in school A be \( 4y \) and the number of girls in school B be \( 5y \) (since the ratio of girls in school A to girls in school B is 4:5).

Since the total number of pupils in both schools is the same, the number of pupils in school A is equal to the number of pupils in school B: \[ 2x + 4y = x + 5y \] Now, solve for \( x \) and \( y \): Subtract \( x \) from both sides: \[ x + 4y = 5y \] Subtract \( 4y \) from both sides: \[ x = y \] Thus, \( x = y \).

Now we substitute \( y = x \) into the number of boys and girls in school A:

Boys in school A = \( 2x \)

Girls in school A = \( 4y = 4x \)

Therefore, the ratio of boys to girls in school A is: \[ \dfrac{\text{Boys in school A}}{\text{Girls in school A}} = \dfrac{2x}{4x} = \dfrac{1}{2} \] The ratio of the boys in school A to the girls in school A is \( 1:2 \).

Let the number of boys be \( 5x \) and the number of girls be \( 6x \), where \( x \) is a common factor. The total number of students is: \[ 5x + 6x = 66 \] \[ 11x = 66 \] Divide both sides by 11: \[ x = 6 \] Now, the number of girls is: \[ 6x = 6 \times 6 = 36 \] There are 36 girls in the class.

Total number of balls in the bag: \[ 5 + 3 + 2 = 10 \] The number of favorable outcomes (red or blue balls): \[ 5 \, (\text{red}) + 2 \, (\text{blue}) = 7 \] The probability is the ratio of favorable outcomes to total outcomes: \[ P(\text{red or blue}) = \dfrac{7}{10} \] The probability is \( \dfrac{7}{10} \).

Let \( L \) be the length of the ladder.

The lader, the wall and the line from the base of the ladder to the wall form a right triangle. Use the Pythagorean theorem: \[ \text{Length}^2 = 6^2 + 8^2 = 36 + 64 = 100 \\ \text{Length} = \sqrt{100} = 10\ \text{meters} \]

The increase in price is: \[ \text{Increase} = 100 - 80 = 20 \] The percent increase is calculated as: \[ \text{Percent Increase} = \left( \dfrac{20}{80} \right) \times 100 = 25\% \] The percent increase is \( 25\% \).

Let the distance Joe drove at each speed be \( d \) miles. Since he drove at two different speeds, we can use the formula for average speed: \[ \text{Average speed} = \dfrac{\text{Total distance}}{\text{Total time}} \] The total distance for the whole trip is the sum of the distances driven at each speed: \[ \text{Total distance} = d + d = 2d \] Now, let's calculate the total time for the trip. The time for the first part of the trip, when Joe drove at 45 miles per hour, is: \[ T_1 = \dfrac{d}{45} \] The time for the second part of the trip, when Joe drove at 55 miles per hour, is: \[ T_2 = \dfrac{d}{55} \] Thus, the total time for the trip is: \[ \text{Total time} = T_1 + T_2 = \dfrac{d}{45} + \dfrac{d}{55} \] To simplify, find a common denominator for the fractions. The least common denominator of 45 and 55 is 495. We rewrite the fractions with this denominator: \[ \dfrac{d}{45} = \dfrac{11d}{495}, \quad \dfrac{d}{55} = \dfrac{9d}{495} \] Now, add the fractions: \[ \text{Total time} = \dfrac{11d}{495} + \dfrac{9d}{495} = \dfrac{20d}{495} \] The average speed is then: \[ \text{Average speed} = \dfrac{2d}{\dfrac{20d}{495}} = 2d \times \dfrac{495}{20d} \] \[ = \dfrac{990}{20} = 49.5 \, \text{miles per hour} \] The average speed for the whole trip is \( 49.5 \) miles per hour.

Let the time taken by Ball A to complete one full rotation be \( T_A \), and the time taken by Ball B to complete one full rotation be \( T_B \).

Ball A makes 2 full rotations in 26 minutes, so the time for one rotation is: \[ T_A = \dfrac{26}{2} = 13 \text{ minutes per rotation} \] Ball B makes 5 full rotations in 35 minutes, so the time for one rotation is: \[ T_B = \dfrac{35}{5} = 7 \text{ minutes per rotation} \] Now, we need to find when both balls will be at the same starting point again. This happens when the time is a common multiple of \( T_A = 13 \) and \( T_B = 7 \). The least common multiple (LCM) of 13 and 7 will give us the time when they both meet at the starting point. Since 13 and 7 are both prime numbers, their LCM is simply their product: \[ \text{LCM}(13, 7) = 13 \times 7 = 91 \text{ minutes} \] The two balls will be at the same starting point again after 91 minutes.

The average of \( x \), \( y \), \( z \), and \( w \) is equal to 25. Hence, \[ \dfrac{x + y + z + w}{4} = 25 \] The average of \( x \), \( y \), and \( z \) is equal to 27. Hence, \[ \dfrac{x + y + z}{3} = 27 \] The above gives \[ x + y + z = 3 \times 27 = 81 \] Substitute \( x + y + z \) by 81 in the equation \( \dfrac{x + y + z + w}{4} = 25 \) to obtain the equation: \[ \dfrac{81 + w}{4} = 25 \] Solve the above for \( w \): \[ 81 + w = 25 \times 4 = 100 \] \[ w = 100 - 81 = 19 \] Hence, \( w = 19 \).

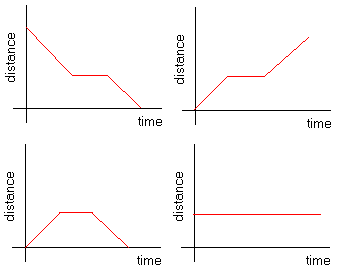
As peter drives away from home, the distance from home should increase. Only the graphs bottom-left and top-right shows an increase at the start (t=0). While shopping the distance stays constant but as he starts driving back the distance must decrease as he approaches home. Therefore only the graph at the bottem-left shows a decrease of distance and best represents the changes in the distance.

The volume of water in the rectangular prism on the left is given by: \[ \text{Volume of rectangular prism} = 2 \times 4 \times 10 = 80\ \text{cm}^3 \] The volume of water in the middle rectangular prism is: \[ \text{Volume of rectangular prism} = 2 \times 4 \times h = 8h \] The volume of water in the cylindrical container on the right is: \[ \text{Volume of cylinder} = \pi \times (1)^2 \times h = \pi h, \quad \pi \approx 3.14 \] Since all the water from the container on the left is poured into both containers on the right, we have: \[ 80 = 8h + \pi h \] Now, solve for \( h \): \[ 80 = h(8 + \pi) \] \[ h = \dfrac{80}{8 + \pi} \] Substitute \( \pi \approx 3.14 \): \[ h = \dfrac{80}{8 + 3.14} = \dfrac{80}{11.14} \approx 7.2\ \text{cm} \] The height \( h \) of the water in both containers is approximately 7.2 cm (rounded to the nearest tenth of a cm).

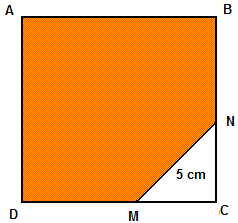
Since the perimeter is equal to 100, the side \( x \) of the square is: \[ x = \dfrac{100}{4} = 25 \] The area \( A \) of the pentagon \( ABNMD \) can be found by subtracting the area of the right triangle \( MNC \) from the total area of the square given by \( x^2 = 25^2 \). \[ A = 25^2 - \dfrac{1}{2} \times MC \times NC \] Since triangle \( MNC \) is isosceles, the lengths of \( NC \) and \( MC \) are equal (\( MC = NC \)), and the above area can be written as: \[ A = 25^2 - \dfrac{1}{2} \times MC^2 \] Also, since triangle \( MNC \) is a right triangle, we can use the Pythagorean theorem to find \( MC^2 \). \[ MC^2 + NC^2 = 5^2 \] Since \( MC = NC \), the above equation becomes: \[ 2 \times MC^2 = 5^2 \] Solving for \( MC^2 \): \[ MC^2 = \dfrac{25}{2} \] Now, substitute \( MC^2 = \dfrac{25}{2} \) into the area \( A \) equation: \[ A = 25^2 - \dfrac{1}{2} \times MC^2 = 25^2 - \dfrac{1}{2} \left( \dfrac{25}{2} \right) \] \[ = 25^2 - \dfrac{25}{4} = 625 - 6.25 \] \[ = 618.75 \, \text{square centimeters} \]

Let \( X \) be the number of cards that cost \$0.25 each and \( Y \) be the number of cards that cost \$0.15 each. The total number of cards is 20. Hence, we have the equation: \[ X + Y = 20 \] If \( X \) is the number of cards at \$0.25, then the cost of \( X \) cards is: \[ 0.25X \] If \( Y \) is the number of cards at \$0.15, then the cost of \( Y \) cards is: \[ 0.15Y \] The total cost of the \( X \) cards and the \( Y \) cards is \$4.2, which gives the equation: \[ 0.25X + 0.15Y = 4.2 \] Now we need to solve the system of equations: \[ X + Y = 20 \quad (1) \] \[ 0.25X + 0.15Y = 4.2 \quad (2) \] Mutliply all terms of equation (2) by 100 and simplify to eliminate decimals: \[ 25 X + 15 Y = 420 \quad (3) \] From equation (1), we can solve for \( Y \): \[ Y = 20 - X \] Substitute \( Y = 20 - X \) into the equation (3) \[ 25 X + 15 (20 - X) = 420 \] Simplify: \[ 25 X + 300 - 15 X = 420 \] Combine like terms: \[ 10 X = 120 \] Divide by 10 and simplify: \[ X = 12 \] Now substitute \( X = 12 \) into the first equation: \[ Y = 20 - 12 = 8 \] The number of cards that cost \$0.25 is \( X = 12 \), and the number of cards that cost \$0.15 is \( Y = 8 \).

Out of the 6 possible numbers that may be rolled, 3 are even: 2, 4, and 6. However, only 4 and 6 are greater than 2. Hence, the probability that the number rolled is an even number greater than 2 is given by: \[ \dfrac{\text{number of even numbers greater than 2}}{6} = \dfrac{2}{6} = \dfrac{1}{3} \]

\[ \text{Volume} = \pi r^2 h = 3.14 \times 4^2 \times 10 \] \[ = 3.14 \times 16 \times 10 = 502.4\ \text{cm}^3 \]