|
|
Solutions with explanations to compass math test practice questions in sample 2.
A - Numerical Skills/Pre-Algebra
-

Solution
Order of operation: inner brackets first
(72 - 9) ÷ 3 ? 2 + 2 = (63)÷ 3 ? 2 + 2
Order of operation: multiplication and division from left to right
= 21 ? 2 + 2
= 42 + 2 = 44
-
In scientific notation, 3.0 x 10-5 + 4.0 x 10-4 =
Solution
Write 3.0 x 10-5 as 3.0 x 10-1 x 10-4 in order to have same power of 10 in the two terms
3.0 x 10-5 + 4.0 x 10-4 = 3.0 x 10-1 x 10-4 + 4.0 x 10-4
= 0.3 x 10-4 + 4.0 x 10-4
= 4.3 x 10 -4
-
If
 . .
is calculated and the fraction obtained reduced to simplest form, then what is its numerator?
Solution
Order of operations: brackets first
1/2 + 1/6 = 3/6 + 1/6 = 4/6
1/3 + 3/4 = 4/12 + 9/12 = 13/12
Substitute and add
2/3 +(1/2 + 1/6) - (1/3 + 3/4) = 2/3 + 4/6 - 13/12
= 8/12 + 8/12 - 13/12 = 3/12 = 1/4
The numerator of the fraction obtained is equal to 1.
-
 . .
Solution
Order of operations: brackets first
4/3 ÷ 3/5 = 4/3 × 5/3 = 20/9
1/4 × 4/5 = 1/5
Substitute in the given expression and simplify
1/5 + (4/3 ÷ 3/5) - (1/4 × 4/5) = 1/5 + 20/9 - 1/5
= 20/9 = 18/9 + 2/9 = 2(2/9) (read as mixed number)
-
A shop owner decreased the selling price of a pair of shoes from $25 to $22. By what percentage was the price decreased?
Solution
change in price = original price - price after reduction = 25 - 22 = 3
Percent change = change / original price = 3/25 = 12/100 = 12%
-
2/5 + 0.4 + 10% =
Solution
If result is sought as a fraction, change to fractions. Hence
0.4 = 4/10 = 2/5
10% = 10 / 100 = 1/10
and
2/5 + 0.4 + 10% = 2/5 + 2/5 + 1/10 = 4/10 + 4/10 + 1/10 = 9/10
-
Linda worked for 8 hours and was paid $6.20 per hour. She then went shopping and bought two boxes of chocolate at $12.50 each and three boxes of cookies at $4.25 each. How much money does Linda have left?
Solution
Linda earned
Money earned = 8 x 6.20 = $49.60
Linda spent
chocolate: 2 x 12.50 = $25
cookies: 3 x 4.25 = $12.75
total = 25 + 12.75 = $37.75
Money left
Money left = Money earned - Money spent = 49.60 - 37.75 = $11.85
-
Jhon bought 2(1/4) pounds of blue cheese, 2.75 pounds of Cheddar cheese and 4(1/2) pounds of goat cheese. How many pounds of cheese did Bill buy?
Solution
Add all quantities of cheese bought
2(1/4) + 2.75 + 4(1/2)
Change 2.75 into fraction
2.75 = 2 + 0.75 = 2 + 3/4 = 2(3/4)
Substitute
2(1/4) + 2.75 + 4(1/2) = 2(1/4) + 2(3/4) + 4(1/2)
= 9/4 + 11/4 + 9/2 = 9/4 + 11/4 + 18/4
= 38/4 = (36 + 2) / 4
= 9(2/4) = 9(1/2)
-
In a factory , 2/5 of all workers earn more than $12 per hour. The number of the workers earning $12 per hour or less is 120. How many workers earn more than $12 per hour?
Solution
There are two groups of workers: those who earn $12 or less and those who earn more than $12.
Let x be the total number of workers. If 2/5 earn more than $12 per hour, then
x - (2/5)x = (5/5)x - (2/5)x
= (3/5)x earn $12 or less and correspond to 120 workers.
Hence
(3/5)x = 120
Solve for x
x = 5*120/3 = 200 , total number of workers
The number of workers who earn more that $12 is 2/5 of the total and is given by
(2/5)200 = 80.
-
40% of students in a school have no brothers or sisters. Of the remaining students, 1/4 have exactly 1 brother or sister. What fraction of all students have more than 1 brother or sister?
Solution
let x be the total number of students in the school. 40% of x has no brother or sister. Hence the remaining students (x - 40% x) have at least one brother or sister.
x - 40% x = x - (40/100) x = x - 0.4 x = 0.6 x , remaining
1/4 of the remaining students have excatly 1 brother or sister.
(1/4) 0.6 x = 0.15 x have exactly one brother or sister.
0.4 x have no brother or sister, 0.15 x have exactly one brother or sister. Hence.
x - (0.4 x + 0.15 x) have more than on brother or sister.
= 0.45 x = (45/100) x
45/100 of the total number of students have more than one brother or sister.
45/100 = 9*5 / 20*5 = 9/20 of all students have more than 1 brother or sister
-
Two different car hire companies offers two different plans: A and B. In plan A, a customer pays a flat fee of $25 for the day plus 10 cents for each kilometer. In plan B, a customer pays 15 cents for each of the first 100 kilometers and 20 cents for each kilometer after the first 100 kilometers. For how many kilometers would a customer pay the same amount for the two plans?
A) 300
B) 100
C) 200
D) 400
E) 120
-
Three workers worked for x hours and earned a total of y dollars. How much will two of these workers earn if they work z hours?(the workers work at the same rate).
A) 3xy / 2z
B) 2z / 3xy
C) 2yz / 3x
D) 6xyz
E) 3yz / 2xy
-
In a test, the 15 girls in the class had an average of 85. The average of the 10 boys in the class was 76? What was the average of the class?
A) 80.5
B) 6.5
C) 80.2
D) 80.3
E) 81.4
-
Find x if 100/x = 10/25.
A) 25
B) 40
C) 25,000
D) 250
E) 2,500
-
√(42 - 32) =
A) √7
B) 5
C) 2 - √3
D) 0
E) 1
B - Algebra
-
If x = -3 and y = -2, what is the value of (x3 - 3) / (y2 - 1)
A) -8
B) -10
C) 8
D) 6
E) -6
-
If -4(x - 5) = -30, then - 2x + 3 =
A) -10
B) -30
C) -20
D) -15
E) -22
-
If 25% of x is equal to 24, then what is 1/12 of x?
A) 1/8
B) 8
C) 1/4
D) 4
E) 2
-
A rectangle of length L and width w has perimeter P and area A. Express A in terms of P and L.
A) L(P - L)
B) L(P -2L)
C) (L/2)(P - 2L)
D) (L/2)(P + 2L)
E) L(P/2 - 2L)
-
Sam spent a 1/4 of his money on a computer system. He bought a bike at $1000 and spent half of what he paid for the computer on food. If x is the initial amount of money that Sam had, then the amount, in dollars, of money left after shopping is given by
A) 0.625x - 1000
B) 0.750x - 1000
C) 0.5x - 1000
D) x - 1000
E) 0.5x - 100
-
Which of the following is equivalent to 7x2 - 27x - 4?
A) (x + 4)(7x - 1)
B) (x - 2)(7x + 2)
C) (x + 2)(7x - 2)
D) (x - 4)(7x + 1)
E) x(7x - 27 - 4)
-
(x - y)3 =
A) x3 - y3
B) x3 - y3 - 2xy
C) x3 - y3 - 3x2y + 3xy2
D) x3 - y3 + 2xy
E) x3 - y3 - 3x2y + 3xy2
-
During the same journey, Stuart drove 160 miles for 2 hours, and 210 miles for 3 hours. Find the average speed for the entire journey.
A) 75 miles/hour
B) 74 miles/hour
C) 150 miles/hour
D) 149 miles/hour
E) 76 miles/hour
-
Given the equations
(I) 2y + 3x = 3
(II) -3y - 2x = 5
(III) -6y + 4x = 9,
(IV) -(2/3)y - x = -1
which two equations are equivalent?
A) (I) and (II)
B) (II) and (III)
C) (III) and (IV)
D) (I) and (IV)
E) (IV) and (II)
-
If f(x - 2) = -(x + 1)2, then f(t - 3) =
A) -(t + 1)2
B) -(t - 2)2
C) - t2
D) -(t - 3)2
E) -(t + 3)2
-
For x < 0, y > 0 and |x| = |y|
|x| + |y| =
A) 0
B) 2x
C) 2y
D) x + y
E) -2y
-
What is the slope of the line whose equation is given by
- y / 4 + 5 = 1
A) -4
B) -1/4
C) -20
D) -5/4
E) 0
-
For x < 2,
1 / (|x - 2|) + 1 / (|2 - x|) =
A) 2 / (2 - x)
B) 0
C) 2 / (x - 2)
D) 1 / (x - 2)
E) 2
-
In a standard rectangular system of axes, what must be x so that the distance between point B(x , 2) and point A(1 , 4) is equal to 2?
A) 0
B) 1
C) 2
D) 3
E) 4
C - College Algebra
-
What is the value of X in the following geometric sequence
X , 64 , ___ , ___ , 1
A) 32
B) 16
C) 64
D) 128
E) 256
-
For what value of A will the system of equations given below have (-2 , 1) as a solution?
2x + 5y = 1
-Ax - y = 5
A) 1
B) -1
C) 0
D) 3
E) 2
-
If f(x) and g(x) are two functions defined by
f(x) = (x + 7)1/2
g(x) = √| 1 - 2 |,
then what is the value of g(f(-3))?
A) 0
B) 1
C) -1
D) undefined
E) -3
-
The range of
f(x) = | x2 - 4 |
is given by the interval
A) (-4 , +infinity)
B) [-4 , +infinity)
C) (4 , +infinity)
D) [4 , +infinity)
E) [0 , +inifinity)
-
If f is a linear function such that f(-1) = 5 and f(2) = -1,
then f(x + 1) =
A) -2x + 1
B) -2x + 3
C) x + 1
D) -2x + 2
E) 2x + 1
-
Which of these functions is (are) always decreasing?
(I) f(x) = -x2 + 2x + 1
(II) f(x) = -2x - 100
(III) f(x) = -|x + 3| - 9
(IV) f(x) = e-x,
A) (I) and (II) only
B) (II) only
C) (II) and (IV) only
D) (I) and (III) only
E) (III) and (IV) only
-
i is the imaginary unit such that i = √-1. What is the value of (i77)2?
A) -1
B) 1
C) i
D) -i
E) 0
-
If
 . .
Find a, b and c.
A) a = -2 , b = 5/2 , c = 15/2
B) a = -3/2 , b = 5/2 , c = 7
C) a = -2 , b = 5/2 , c = 7
D) a = 2 , b = 5/2 , c = 7
E) a = -2 , b = 5/2 , c = -15/2
-
In an arithmetic series, the first term is equal to 0.5 and the 10th term is equal to 2.75. Find the sum of the first 20 terms in the series.
A) 58
B) 58.25
C) 5.75
D) 57.5
E) 32.5
D - Geometry
-
In the figure below, line T1 is parallel to line T2 and line L1 is parallel to line L2. What is the measure of angle f if the measure of angle i is 127 degrees?
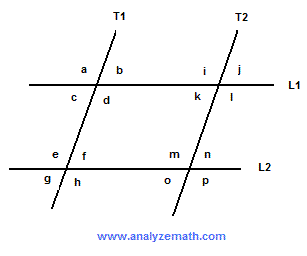 . .
A) 127 degrees
B) 37 degrees
C) 45 degrees
D) 50 degrees
E) 53 degrees
-
The measures of two sides of a triangle are x and 2x. The angle made by these two sides is equal to 30 degrees. What is the area of the triangle in terms of x?
A) 2 x2
B) 0.5 x2
C) x2
D) 3 x2
E) Cannot be calculated
-
Find the circumference of a circle whose diameter has endpoints at (2 , 1) and (4 , 5).
A) 5
B) 20 Pi
C) 10 Pi
D) 15 Pi
E) 5 Pi
-
The ratio of the perimeters of two circles is equal to 5. What is the ratio of their areas?
A) 5
B) 10
C) 25
D) 25 Pi
E) 5 Pi2
-
In the figure below, EB and FC are both perpendicular to AC and x is the length of AB. If the length of AF is 15, what is x?
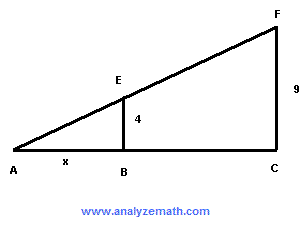 . .
A) 16 / 3
B) 256 / 9
C) 4
D) 32 / 3
E) 16 / 9
-
An isosceles right triangle has an area of 50 cm2. Find the perimeter of this triangle.
A) 30 cm
B) 100 cm
C) 20 + 10sqrt(2) cm
D) 20 + 2sqrt(10) cm
E) 20 + sqrt(10) cm
-
AB is the diameter of a semicircle and C is an arbitrary point on the semicircle (other than A or B), and o is the center of the circle inscribed into triangle ABC. Find the the measure of angle AoB.
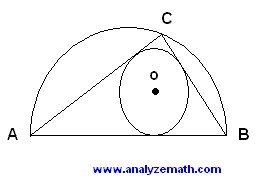 . .
A) 90 degrees
B) 135 degrees
C) 45 degrees
D) 100 degrees
E) 120 degrees
-
A rectangle of length L and width W and a square of side x have equal perimeters. The length L is 10 more than x. Express W in terms of x.
A) W = x
B) W = 2x
C) W = x - 5
D) W = x - 10
E) W = x + 10
-
The area of a square field is 200 m2. What is the diagonal of this field?
A) 20 m
B) 10 sqrt(2) m
C) 100 m
D) 50 sqrt(2) m
E) 10 m
E - Trigonometry
-
If x is a positive angle smaller than 90° and tan(x) = 3, then cos(x) =
A) 1 / 3
B) 1 / sqrt(8)
C) 1 / 10
D) 1 / sqrt(10)
E) 1
-
Convert 23?/3 into degrees.
A) 60 degrees
B) 1380 degrees
C) 690 degrees
D) 2070 degrees
E) 180 degrees
-
The measurement of an angle of a right triangle is 30° and the leg adjacent to this angle is 10 cm long. What is perimeter of the triangle?
A) 30 cm
B) 40 sqrt(3) cm
C) 20(1 + sqrt(3)) cm
D) 30(1 + sqrt(3)) cm
E) 10(1 + sqrt(3)) cm
-
Which of these graphs is the graph of y = cos((1/2)x)?
 . .
-
What is the smallest positive value of x for which y = sin(3x + pi/2) has a maximum value?
A) Pi / 2
B) 5 Pi / 2
C) 2 Pi / 3
D) Pi / 3
E) Pi / 6
-
The area of the regular hexagon shown below is 100 cm2. What is the length x of the side of the hexagon?
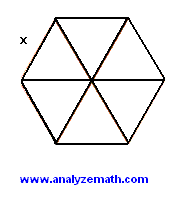 . .
A) 6.2 cm
B) 38.5 cm
C) 16.6 cm
D) 8.3 cm
E) 12.4 cm
Answers to the Above Questions
- E
- B
- A
- D
- C
- E
- A
- B
- B
- E
- A
- C
- E
- D
- A
- B
- E
- B
- C
- A
- D
- E
- B
- D
- C
- C
- E
- A
- B
- E
- D
- B
- E
- B
- C
- A
- C
- D
- E
- B
- E
- C
- A
- C
- B
- D
- A
- D
- B
- E
- D
- C
- A
More ACT, SAT and Compass practice
|
|