Multiply Fractions Concept - Grade 5
The concept of multiplying fractions is explained using examples then the rule is given.
Examples with Solutions
Example 1
Let us explain how do the following multiplication \( \dfrac{1}{2} \times \dfrac{1}{3 } \)
We start with a rectangle. We use a picture to represent \( \dfrac{1}{3 } \) (in red).
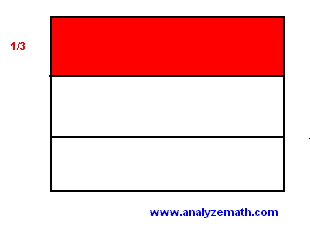 .
.
We now take \( \dfrac{1}{2} \) of the red part (blue). The blue part which is \( \dfrac{1}{2} \) of \( \dfrac{1}{3} \) is also \( \dfrac{1}{6} \) of the unit we started with. We can write
\[ \dfrac{1}{2} \times \dfrac{1}{3 } = \dfrac{1}{6} \]
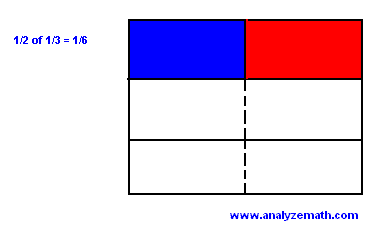 .
.
Example 2
Let us explain how do the following multiplication \( \dfrac{1}{3} \times \dfrac{3}{4} \)
We start with a rectangle. We use a picture to represent \( \dfrac{3}{4} \) (in red).
 .
.
We now take \( \dfrac{1}{3} \) of the red part (blue). The blue part which is \( \dfrac{1}{3} \) of \( \dfrac{3}{4} \) is also \( \dfrac{3}{12} \) of the unit we started with. We can write
\[ \dfrac{1}{3} \times \dfrac{3}{4} = \dfrac{3}{12} \]
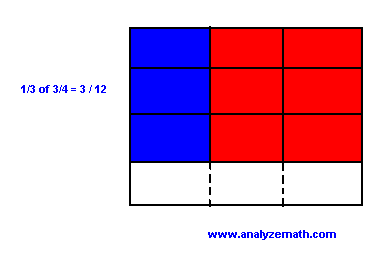 .
.
General Rule of Multiplication of Fractions
\[ \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{a \times c}{b \times d} = \dfrac{a \times c}{b \times d} \]
multiply numerators and denominators.
Example 3
Evaluate
a) \( \dfrac{2}{3} \times \dfrac{5}{3} \)
b) \( \dfrac{3}{10} \times \dfrac{5}{21} \)
Solution to Example 3
a) \( \dfrac{2}{3} \times \dfrac{5}{3} = \dfrac{2 \times 5}{3 \times 3} = \dfrac{10}{9} \)
b) \( \dfrac{3}{10} \times \dfrac{5}{21} = \dfrac{3 \times 5}{10 \times 21} = \dfrac{15}{210} \)
 .
.
 .
.
 .
.
 .
.