Este es un tutorial sobre cómo resolver ecuaciones cuadráticas gráficamente y verificar las respuestas analíticamente. Las ecuaciones cuadráticas exploradas son del tipo:
\[ ax^2 + bx + c = 0 \]
Las soluciones analíticas de una ecuación cuadrática vienen dadas por la fórmula cuadrática:
\[ x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a} \]
donde \(\Delta = b^2 - 4ac\) se llama discriminante. Proporciona información sobre el número y tipo de soluciones:
Las soluciones gráficas se obtienen graficando la función \(y = ax^2 + bx + c\). Las intersecciones con el eje x, si existen, proporcionan soluciones aproximadas.
Resolver gráfica y analíticamente:
\[2x^2 + 3x = 5\]Reescribir en forma estándar:
\[ 2x^2 + 3x - 5 = 0 \]
Graficar la función:
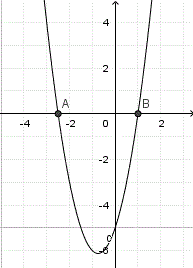
\[ y = 2x^2 + 3x - 5 \]
Ubicar las intersecciones con el eje x: \(x_1 \approx -2.5\), \(x_2 \approx 1\).

Discriminante:
\[ \Delta = b^2 - 4ac = 3^2 - 4(2)(-5) = 49 \]
Dado que \(\Delta > 0\), existen dos soluciones reales:
\[ x_1 = \frac{-3 + \sqrt{49}}{2\cdot 2} = 1, \quad x_2 = \frac{-3 - \sqrt{49}}{2\cdot 2} = -2.5 \]
Las soluciones gráfica y analítica coinciden. Las soluciones gráficas son aproximadas en general.
Resolver gráfica y analíticamente:
\[ x^2 + 4x + 4 = 0 \]Graficar la función:
\[ y = x^2 + 4x + 4 \]
Hay una intersección con el eje x: \(x = -2\).

Discriminante:
\[ \Delta = b^2 - 4ac = 16 - 16 = 0 \]
Dado que \(\Delta = 0\), existe una solución:
\[ x = \frac{-b}{2a} = \frac{-4}{2 \cdot 1} = -2 \]
Resolver gráfica y analíticamente:
\[ -x^2 + 4x - 5 = 0 \]Graficar la función:
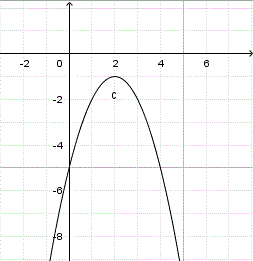
\[ y = -x^2 + 4x - 5 \]
No hay intersecciones con el eje x; no hay soluciones reales, solo complejas.
Discriminante:
\[ \Delta = b^2 - 4ac = 4^2 - 4(-1)(-5) = -4 \]
Dado que \(\Delta < 0\), existen dos soluciones complejas conjugadas:
\[ x_1 = \frac{-4 + \sqrt{-4}}{2(-1)} = 2 - i, \quad x_2 = \frac{-4 - \sqrt{-4}}{2(-1)} = 2 + i \]
El método gráfico no puede encontrar soluciones imaginarias.
Resolver gráfica y analíticamente: