La diferenciación se utiliza para analizar las propiedades tales como intervalos de aumento, disminución, máximo local, mínimo local de las funciones cuadráticas.
Las funciones cuadráticas en su forma general se escriben como
\[f(x) = ax^2 + bx + c\]donde \(a\), \(b\), y \(c\) son números reales tales que \(a \neq 0\).
La primera derivada de \(f\) está dada por
\[f'(x) = 2ax + b\]Analicemos el signo de \(f'\) y determinemos cualquier punto máximo o mínimo y los intervalos de aumento y disminución. \(f'(x)\) es positiva si
\[2ax + b > 0\] lo cual se puede escribir como \[2 a x > - b\]Ahora necesitamos considerar dos casos y continuar resolviendo la desigualdad anterior.
Dividimos ambos lados de la desigualdad por \(2a\) y la resolvemos para obtener
\[x > -\frac{b}{2a}\]Ahora usamos una tabla para analizar el signo de \(f'\) y si \(f\) está aumentando sobre un intervalo dado.
La función cuadrática con \(a > 0\) tiene un punto mínimo en \((-b/2a, f(-b/2a))\) y la función está disminuyendo en el intervalo \((- \infty, -b/2a)\) y aumentando en el intervalo \((-b/2a, + \infty)\).
Dividimos ambos lados de la desigualdad por \(2a\) pero como \(a\) es menor que 0, necesitamos cambiar el símbolo de la desigualdad
\[x \lt -\frac{b}{2a}\]Ahora analizamos el signo de \(f'\) usando la siguiente tabla
La función cuadrática con \(a \lt 0\) tiene un punto máximo en \((-b/2a, f(-b/2a))\) y la función está aumentando en el intervalo \((- \infty, -b/2a)\) y disminuyendo en el intervalo \((-b/2a, + \infty)\).
Las funciones cuadráticas en su forma del vértice se escriben como
\[f(x) = a(x - h)^2 + k\]donde \(a\), \(h\), y \(k\) son números reales con \(a \neq 0\).
La primera derivada de \(f\) está dada por
\[f'(x) = 2a(x - h)\]Analicemos el signo de \(f'\) usando una tabla. \(f'(x)\) es positiva si
\[a(x - h) > 0\]Necesitamos considerar dos casos nuevamente y continuar resolviendo la desigualdad anterior.
Dividimos ambos lados de la desigualdad por \(a\) y resolvemos la desigualdad
\[x > h\]La tabla a continuación se utiliza para analizar el signo de \(f'\).
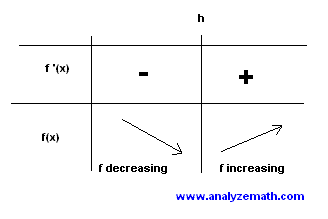
La función cuadrática con \(a > 0\) tiene un mínimo en el punto \((h, k)\) y está disminuyendo en el intervalo \((- \infty, h)\) y aumentando en el intervalo \((h, + \infty)\).
Dividimos ambos lados de la desigualdad por \(a\) pero necesitamos cambiar el símbolo de la desigualdad porque \(a\) es menor que 0.
\[x \lt h\]Analicemos el signo de \(f'\) usando la tabla siguiente
La función cuadrática con \(a < 0\) tiene un punto máximo en \((h, k)\) y la función está aumentando en el intervalo \((- \infty, h)\) y disminuyendo en el intervalo \((h, + \infty)\).
Encuentra el extremo (mínimo o máximo) de la función cuadrática \(f\) dada por
\[f(x) = 2x^2 - 8x + 1\]
Encuentra el extremo (mínimo o máximo) de la función cuadrática \(f\) dada por
\[f(x) = - (x + 3)^2 + 1\]
a) \(f(x) = x^2 + 6x\)
b) \(f(x) = -x^2 - 2x + 3\)
c) \(f(x) = x^2 - 5\)
d) \(f(x) = -(x - 4)^2 + 2\)
e) \(f(x) = -x^2\)
aplicaciones de la diferenciación
