Tutorial on Discrete Probability Distributions

Tutorial on discrete probability distributions with examples and detailed solutions.

Discrete Probability Distribution

Let X be a discrete random variable that takes the numerical values X1, X2, ..., Xn with probabilities p(X1), p(X2), ..., p(Xn) respectively. A discrete probability distribution consists of the values of the random variable X and their corresponding probabilities P(X).
The probabilities P(X) are such that
∑ P(X) = 1

Example 1

Let the random variable X represents the number of boys in a family.
a) Construct the probability distribution for a family of two children.
b) Find the mean and standard deviation of X.

Solution to Example 1

a) We first construct a tree diagram to represent all possible distributions of boys and girls in the family.
Assuming that all the above possibilities are equally likely, the probabilities are:
P(X=2) = P(BB) = 1 / 4
P(X=1) = P(BG) + P(GB) = 1 / 4 + 1 / 4 = 1 / 2
P(X=0) = P(GG) = 1 / 4
The discrete probability distribution of X is given by

X P(X)

0 1 / 4

1 1 / 2

2 1 / 4
Note that
∑ P(X) = 1
b) The mean µ of the random variable X is defined by
μ = ∑ X P(X)
= 0 * (1/4) + 1 * (1/2) + 2 * (1/4) = 1
The standard deviation σ of the random variable X is defined by
σ = √ [ ∑ (X- µ)² P(X) ]
= √ [ (0 - 1)² * (1/4) + (1 - 1)² * (1/2) + (2 - 1)² * (1/4) ]
= 1 / √ (2)

X	P(X)
0	1 / 4
1	1 / 2
2	1 / 4

Example 2

Two balanced dice are rolled. Let X be the sum of the two dice.
a) Obtain the probability distribution of X.
b) Find the mean and standard deviation of X.

Solution to Example 2

a) When the two balanced dice are rolled, there are 36 equally likely possible outcomes as shown below .
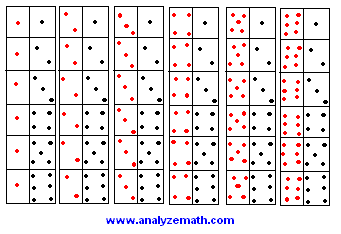
The possible values of X are: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.
The possible outcomes are equally likely hence the probabilities P(X) are given by
P(2) = P(1,1) = 1 / 36
P(3) = P(1,2) + P(2,1) = 2 / 36 = 1 / 18
P(4) = P(1,3) + P(2,2) + P(3,1) = 3 / 36 = 1 / 12
P(5) = P(1,4) + P(2,3) + P(3,2) + P(4,1) = 4 / 36 = 1 / 9
P(6) = P(1,5) + P(2,4) + P(3,3) + P(4,2) + P(5,1)= 5 / 36
P(7) = P(1,6) + P(2,5) + P(3,4) + P(4,3) + P(5,2) + P(6,1)
= 6 / 36 = 1 / 6
P(8) = P(2,6) + P(3,5) + P(4,4) + P(5,3) + P(6,2) = 5 / 36
P(9) = P(3,6) + P(4,5) + P(5,4) + P(6,3) = 4 / 36 = 1 / 9
P(10) = P(4,6) + P(5,5) + P(6,4) = 3 / 36 = 1 / 12
P(11) = P(5,6) + P(6,5) 2 / 36 = 1 / 18
P(12) = P(6,6) = 1 / 36
The discrete probability distribution of X is given by

X P(X)

2 1 / 36

3 1 / 18

4 1 / 12

5 1 / 9

6 5 / 36

7 1 / 6

8 5 / 36

9 1 / 9

10 1 / 12

11 1 / 18

12 1 / 36

The graph of the probability of the sum of two dice is shown below.
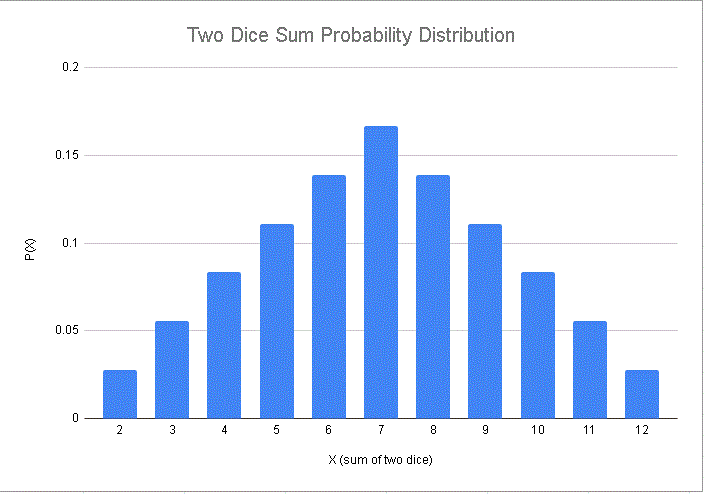
As an exercise, check that
∑ P(X) = 1
b) The mean of X is given by
µ = ∑ X P(X)
= 2*(1/36)+3*(1/18)+4*(1/12)+5*(1/9)+6*(5/36)
+7*(1/6)+8*(5/36)+9*(1/9)+10*(1/12)
+11*(1/18)+12*(1/36)
= 7
The standard deviation of is given by
µ = σ √ [ ∑ (X- µ)² P(X) ]
= √ [ (2-7)²*(1/36)+(3-7)²*(1/18)
+(4-7)²*(1/12)+(5-7)²*(1/9)+(6-7)²*(5/36)
+(7-7)²*(1/6)+(8-7)²*(5/36)+(9-7)²*(1/9)
+(10-7)²*(1/12)+(11-7)²*(1/18)+(12-7)²*(1/36) ]
= 2.41

X	P(X)
2	1 / 36
3	1 / 18
4	1 / 12
5	1 / 9
6	5 / 36
7	1 / 6
8	5 / 36
9	1 / 9
10	1 / 12
11	1 / 18
12	1 / 36

Example 3

Three coins are tossed. Let X be the number of heads obtained. Construct a probability distribution for X and find its mean and standard deviation.

Solution to Example 3

The tree diagram representing all possible outcomes when three coins are tossed is shown below.
Assuming that all three coins are indentical and all possible outcomes are equally likely, the probabilities are:
P(X=0) = P(TTT) = 1 / 8
P(X=1) = P(HTT) + P(THT) + P(TTH)
= 1 / 8 + 1 / 8 + 1 / 8
= 3 / 8
P(X=2) = P(HHT) + P(HTH) + P(THH)
= 1 / 8 + 1 / 8 + 1 / 8
= 3 / 8
P(X=3) = P(HHH) = 1 / 8
The discrete probability distribution of X is given by

X P(X)

0 1 / 8

1 3 / 8

2 3 / 8

3 1 / 8
Note that
∑ P(X) = 1
We now compute the mean µ of the random variable X as follows
µ = ∑ X P(X)
= 0 * (1/8) + 1 * (3/8) + 2 * (3/8) + 3 * (1/8) = 1.5
We now compute the standard deviation σ of the random variable X as follows
σ = √ [ ∑ (X- µ)² P(X) ]
= √ [ (0 - 1.5)² * (1/8) + (1 - 1.5)² * (3/8) + (2 - 1.5)² * (3/8) + (3 - 1.5)² * (1/8) ]
= 0.87 (rounded to 2 decimal places)