Linear Regression
Problems with Solutions

Linear regression and modelling problems are presented along with their solutions at the bottom of the page. Also a linear regression calculator and grapher may be used to check answers and create more opportunities for practice.

Review

If the plot of n pairs of data (x , y) for an experiment appear to indicate a "linear relationship" between y and x, then the method of least squares may be used to write a linear relationship between x and y.
The least squares regression line is the line that minimizes the sum of the squares (d1 + d2 + d3 + d4) of the vertical deviation from each data point to the line (see figure below as an example of 4 points).
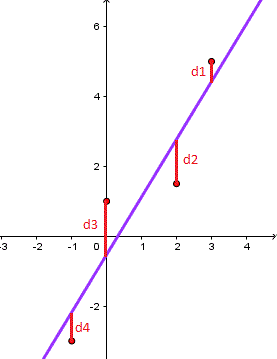
Linear regression where sum of vertical distances between observed and predicted values is minimized.

Figure 1. Linear regression where the sum of vertical distances d1 + d2 + d3 + d4 between observed and predicted (line and its equation) values is minimized.
The least square regression line for the set of n data points is given by the equation of a line in slope intercept form:
y = a x + b

where a and b are given by
linear regression formulas.

Figure 2. Formulas for the constants a and b included in the linear regression .

  • Problem 1

    Consider the following set of points: {(-2 , -1) , (1 , 1) , (3 , 2)}
    a) Find the least square regression line for the given data points.
    b) Plot the given points and the regression line in the same rectangular system of axes.

  • Problem 2

    a) Find the least square regression line for the following set of data
    {(-1 , 0),(0 , 2),(1 , 4),(2 , 5)}

    b) Plot the given points and the regression line in the same rectangular system of axes.

  • Problem 3

    The values of y and their corresponding values of y are shown in the table below
    x 0 1 2 3 4
    y 2 3 5 4 6

    a) Find the least square regression line y = a x + b.
    b) Estimate the value of y when x = 10.

  • Problem 4

    The sales of a company (in million dollars) for each year are shown in the table below.
    x (year) 2005 2006 2007 2008 2009
    y (sales) 12 19 29 37 45

    a) Find the least square regression line y = a x + b.
    b) Use the least squares regression line as a model to estimate the sales of the company in 2012.

Solutions to the Above Problems

  1. a) Let us organize the data in a table.
    x y x y x 2
    -2 -1 2 4
    1 1 1 1
    3 2 6 9
    Σx = 2 Σy = 2 Σxy = 9 Σx2 = 14

    We now use the above formula to calculate a and b as follows
    a = (nΣx y - ΣxΣy) / (nΣx2 - (Σx)2) = (3*9 - 2*2) / (3*14 - 22) = 23/38
    b = (1/n)(Σy - a Σx) = (1/3)(2 - (23/38)*2) = 5/19
    b) We now graph the regression line given by y = a x + b and the given points.
    regression line graph problem 1

    Figure 3. Graph of linear regression in problem 1.
  2. a) We use a table as follows
    x y x y x 2
    -1 0 0 1
    0 2 0 0
    1 4 4 1
    2 5 10 4
    Σx = 2 Σy = 11 Σx y = 14 Σx2 = 6

    We now use the above formula to calculate a and b as follows
    a = (nΣx y - ΣxΣy) / (nΣx2 - (Σx)2) = (4*14 - 2*11) / (4*6 - 22) = 17/10 = 1.7
    b = (1/n)(Σy - a Σx) = (1/4)(11 - 1.7*2) = 1.9
    b) We now graph the regression line given by y = ax + b and the given points.
    regression line graph problem 2

    Figure 4. Graph of linear regression in problem 2.
  3. a) We use a table to calculate a and b.
    x y x y x 2
    0 2 0 0
    1 3 3 1
    2 5 10 4
    3 4 12 9
    4 6 24 16
    Σx = 10 Σy = 20 Σx y = 49 Σx2 = 30

    We now calculate a and b using the least square regression formulas for a and b.
    a = (nΣx y - ΣxΣy) / (nΣx2 - (Σx)2) = (5*49 - 10*20) / (5*30 - 102) = 0.9
    b = (1/n)(Σy - a Σx) = (1/5)(20 - 0.9*10) = 2.2
    b) Now that we have the least square regression line y = 0.9 x + 2.2, substitute x by 10 to find the value of the corresponding y.
    y = 0.9 * 10 + 2.2 = 11.2
  4. a) We first change the variable x into t such that t = x - 2005 and therefore t represents the number of years after 2005. Using t instead of x makes the numbers smaller and therefore manageable. The table of values becomes.
    t (years after 2005) 0 1 2 3 4
    y (sales) 12 19 29 37 45

    We now use the table to calculate a and b included in the least regression line formula.
    t y t y t 2
    0 12 0 0
    1 19 19 1
    2 29 58 4
    3 37 111 9
    4 45 180 16
    Σx = 10 Σy = 142 Σxy = 368 Σx2 = 30

    We now calculate a and b using the least square regression formulas for a and b.
    a = (nΣt y - ΣtΣy) / (nΣt2 - (Σt)2) = (5*368 - 10*142) / (5*30 - 102) = 8.4
    b = (1/n)(Σy - a Σx) = (1/5)(142 - 8.4*10) = 11.6
    b) In 2012, t = 2012 - 2005 = 7
    The estimated sales in 2012 are: y = 8.4 * 7 + 11.6 = 70.4 million dollars.

More References and links

  1. Linear Regression Calculator and Grapher.
  2. Linear Least Squares Fitting.
  3. elementary statistics and probabilities.