Mutually Exclusive Events - Examples With Solutions
Tutorial on finding out whether two given events are mutually exclusive. However a quick review of sample space of an experiment and the events related to a sample space may be necessary.
Two Mutually Exclusive Events
Two events are mutually exclusive if they cannot occur at the same time.
Using Venn diagram, two events that are mutually exclusive may be represented as follows:
The two events are such that
E1 ∩ E2 = Φ
The two sets E1 and E2 have no elements in common and their intersection is an empty set since they cannot occur at the same time.
Using Venn diagram, two events that are not mutually exclusive may be represented as follows:
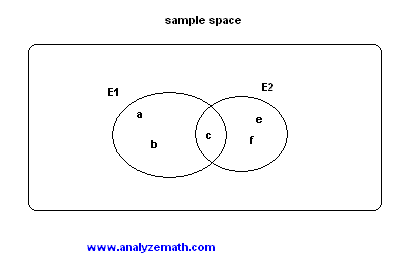E1 ∩ E2 = {c} , the intersection of the two events E1 and E2 is not an empty set
Examples with Solutions
Example 1:
A die is rolled. Let us define event E1 as the set of possible outcomes where the number on the face of the die is even and event E2 as the set of possible outcomes where the number on the face of the die is odd. Are event1 E1 and E2 mutually exclusive?
Solution to Example 1:
We first list the elements of E1 and E2.
E1 = {2,4,6}
E2 = {1,3,5}
E1 and E2 have no elements in common and therefore are mutually exclusive.
Another way to answer the above question is to note is that if you roll a die, it shows a number that is either even or odd but no number will be even and odd at the same time. Hence E1 and E2 cannot occur at the same time and are therfore mutually exclusive.
Example 2:
A die is rolled. Event E1 is the set of possible outcomes where the number on the face of the die is even and event E2 as the set of possible outcomes where the number on the face of the die is greater than 3. Are event E1 and E2 mutually exclusive?
Solution to Example 2:
The subsets E1 and E2 are given by.
E1 = {2,4,6}
E2 = {4,5,6}
Subsets E1 and E2 have 2 elements in common. If the die shows 4 or 6, both events E1 and E2 will have occured at the same time and therefore E1 and E2 are not mutually exclusive.
Example 3:
A card is drawn from a deck of cards. Events E1, E2, E3, E4 and E5 are defined as follows:
E1: Getting an 8
E2: Getting a king
E3: Getting a face card
E4: Getting an ace
E5: Getting a heart
a) Are events E1 and E2 mutually exclusive?
b) Are events E2 and E3 mutually exclusive?
c) Are events E3 and E4 mutually exclusive?
d) Are events E4 and E5 mutually exclusive?
e) Are events E5 and E1 mutually exclusive?
Solution to Example 3:
The sample space of the experiment "card is drawn from a deck of cards" is shown below.
a) E1 and E2 are mutually exclusive because there are no cards with an 8 and a king together.
b) E2 and E3 are not mutually exclusive because a king is a face card.
c) E3 and E4 are mutually exclusive because an ace is not a face card.
d) E4 and E5 are not mutually exclusive because there is one card that has an ace and a heart.
d) E5 and E1 are not mutually exclusive because there is one card that is an 8 of heart.
Example 4: Two dice are rolled. We define events E1, E2, E3 and E4 as follows
E1: Getting a sum equal to 10
E2: Getting a double
E3: Getting a sum less than 4
E4: Getting a sum less to 7
a) Are events E1 and E2 mutually exclusive?
b) Are events E2 and E3 mutually exclusive?
c) Are events E3 and E4 mutually exclusive?
d) Are events E4 and E1 mutually exclusive?
Solution to Example 4:
The sample space of the experiment "2 dice" is shown below.
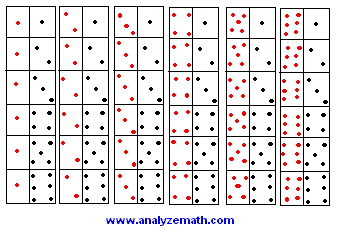
a) E1 and E2 are not mutually exclusive because outcome (5,5) is a double and also gives a sum of 10. The two events may occur at the same time.
b) E2 and E3 are not mutually exclusive because outcome (1,1) is a double and gives a sum of 2 and is less than 4. The two events E2 and E3 may occur at the same time.
c) E3 and E4 are not mutually exclusive a sum can be less than 7 and less than 4 a the same time. Example outcome (1,2).
d) E4 and E1 are mutually exclusive because a sum less than 7 cannot be equal to 10 at the same time. The two events cannot occur at the same time.
