Dot Product of Two Vectors and Applications
Tutorial on the calculation and applications of the dot product of two vectors.
Dot Product of Two Vectors
Knowing the coordinates of two vectors v = < v1 , v2 > and u = <u1 , u2> , the dot product of these two vectors, denoted v . u, is given by:NOTE that the result of the dot product is a scalar .
Example 1: Vectors v and u are given by their components as follows
v = < -2 , 3> and u = < 4 , 6>
Find the dot product v · u of the two vectors.
Solution to example 1:
v · u = < -2 , 3> . <4 , 6>
= (-2) × (4) + (3) × (6) = -8 + 18 = 10
Properties of the Dot Product
1. v · u = u · v2. v · (u + w) = v · u + v · w
3. v · v = || v || 2
4. c(v · u) = cv · u = v · cu
Example 2: Find || v || first using the definition || v || = √( v1 2 + v1 2 ) and then using property 3 above where v = <3 , - 4>
Solution to example 2:
1. definition: || v || = √( v1 2 + v1 2 ) = √( (3) 2 + (- 4) 2 )
= √(9 + 16) = 5
2. Property 3: || v || 2 = v · v
= <3 , - 4> . <3 , - 4> = (3) × (3) + (- 4) × (- 4) = 25
Take the square root to find || v || = 5
Alternative Form of the Dot Product of Two Vectors
In the figure below, vectors v and u have same initial point the origin O(0,0). Points A and B are the terminal points. t is the angle made by the two vectors. Applying the cosine law to triangle OAB, we obtain:d(A,B) 2 = || v || 2 + || u || 2 -2|| v || || u || cos (t)
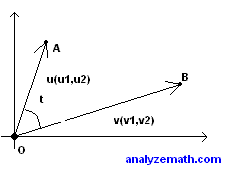
Use the definition of the distance to find d(A,B) and the definition of the magnitude to find || v || and || u || and substitute in the above
(v1 - u1) 2 + (v2 - u2) 2 = (v1 2 + v2 2 ) + (u1 2 + u2 2 ) -2 || v |||| u || cos (t)
Expand the squares in the left side and simplify to obtain
v1 u1 + v2 u2 = || v || || u || cos (t)
The left side is the dot product of vectors v and u, hence
v · u = || v || || u || cos (t)
We may use the above property of the dot product to find angle t between two vectors
cos t = v · u / (|| v || || u ||)
NOTE that if cos t = 0 ( t = Pi / 2) the dot product v . u = 0. This leads to:
vectors v and u are orthogonal if and only if v · u = 0. Example 3: Show that vectors v = <3 , - 4> and u = <4 , 3> are orthogonal
Solution to example 3:
Find dot product v · u
v · u = <3 , - 4> . <4 , 3> = (3)*(4) + (-4)*(3) = 0
according to above
cos t = v · u / (|| v || || u ||) = 0
cos t = 0 means that t = Pi / 2 and the two vectors are orthogonal.
Example 4: Find the angle between vectors v = <1 , 1> and u = < - 4 , 3>.
Solution to example 4:
Find dot product v · u
v · u = <1 , 1> . < - 4 , 3> = (1)*(- 4) + (1)*(3) = - 1
Find || v || and || u ||
|| v || = √(1 2 + 1 2) = √ (2)
|| u || = √((-4) 2 + 3 2) = √ (25) = 5
We now use the formula cos t = v . u / (|| v || || u ||) to find cos t
cos t = v · u / (|| v || || u ||) = - 1 / [ √(2)*5 ]
t = arccos (- 1 / [ √(2)*5 ]) (approximately) = 98.1 o
Exercises
1. Given vectors
v = <10 , - 5> and u = <2 , u2>,
Find u2 so that vectors v and u are orthogonal.
2. Find the angle between vectors v and u given below
v = <1 , 1> and u = <-2 , -2>,
Answers to above exercises
1. u2 = 4
2. 180 o

