Absolute Value Functions

The absolute value function is explored through definitions, examples and exercises with solutions at the bottom of the page. The graphing of absolute value functions |f(x)| is discussed through examples.

Definition of Absolute Value

Absolute Value and Square Root

Properties of the Absolute Value Function

1. \( | x | \ge 0 \)
2. \( \sqrt{ x^2} = | x | \)
3. \( | x | = | - x | \)
4. \( | a b | = | a || b | \)
5. \( \left | \dfrac{a}{b} \right | = \dfrac{|a|}{|b|} , b \ne 0\)

Equations and Inequalities with Absolute Value

1. \( | x | = k \iff x = k \text{ or } x = - k \)
2. \( | x | \le k \iff - k \le x \le k \)
3. \( | x | ? k \iff x \le - k \text{ or } x \ge k \)

Graph of Absolute Value of a Function

1. click on the button above "draw" to start.
   
2. Use the sliders to set parameter a to zero, parameter b to zero and parameter c to a positive value; \( f(x)\) is a constant function. Compare the graph of f(x) in blue and that of \( h(x)= |f(x)| \) in red. Change c to a negative value and compare the graphs again. Use the definition of the absolute value functions to explain how can the graph of \( |f(x)| \) be obtained from the graph of \( f(x)\).
   
3. Keep the value of a equal to zero, select non zero values for b to obtain a linear function . How can the graph of \( h(x) = |f(x)|\) be obtained from that of \( f(x)\)?
   Hint: use the definition of the absolute value functions and reflection of a graph on the x-axis.
   
4. Set b and c to zero and select a positive value for a to obtain a quadratic function . Why are the two graphs the same? (Hint: use the definition of the absolute value functions).
   
5. Set b and c to zero and select a negative value for a to obtain a quadratic function . Why are the two graphs reflection of each other? (Hint: use the definition of the absolute value functions and reflection of a graph on the x-axis).
   
6. Keep the values of a and b as in 5 above and change gradually c from zero to some positive values. How can the graph of \( h(x)=|f(x)|\) be obtained from that of \( f(x)\)?
   
7. Select different values for a, b and c and explore.
   

Exercises

1. | - 9 |
   
2. | 9 |
   
3. | 2 - 6 |
   
4. \( |- \dfrac{5}{2}| \)
   
5. \( | 11 - 4^2 | \)
   
6. \( 2^{| 2 - 7|} \)
   
7. \( |2-19| - |9 - 20| \)

1. | x - 10 | + | 2 x | , x = - 7
   
2. | - x | , x = 8
   
3. \( \left |- \dfrac{|x - 2|}{|-x + 9|} \right | \) , x = -20
   
4. \( | - 3 x - x^2 | \) , x = -3
   
5. \( x^{| x - 7|} \) , x = - 2

1. | a - b | for a = b
   
2. | a - b | for a > b
   
3. | a - b | for b > a
4. \( \sqrt {3^2} \)
5. \( \sqrt {(- 3)^2} \)
6. \( \sqrt { (12 - 20)^2 } \)
7. \( | x^2 | \)
8. \( | (-x)^2 | \)
9. \( | (x + 1)^2 | \)
10. \( \sqrt{(x - y + z)^2} \)
11. \( \sqrt{sin^2(x)} \)

1. \( |x - 2| = 4 \)
2. \( |x + 5| = 0 \)
3. \( |10 - x| = - 5 \)

1. \( |x - 7| \gt 4 \)
2. \( |x + 5| \lt 9 \)
3. \( |x + 8| \lt - 5 \)
4. \( |x + 8| \gt - 2 \)

1. \( f(x) = x - 1 , h(x) = |f(x)| \)
   
2. \( f(x) = x^2 - 4 , h(x) = |f(x)| \)
   
3. \( f(x) = \sin(x) , h(x) = |\sin(x)| \)

Solutions to the Above Exercises
Part 1
Evaluate the expressions

1. | - 9 | = 9
   
2. | 9 | = 9
   
3. | 2 - 6 | = 4
   
4. \( |- \dfrac{5}{2}| = \dfrac{5}{2} \)
   
5. \( | 11 - 4^2 | = 5 \)
   
6. \( 2^{| 2 - 7|} = 32 \)
   
7. \( |2-19| - |9 - 20| = 6 \)

1. For x = - 7, | x - 10 | + | 2 x | = 31
   
2. For x = 8 , | - x | = 8
   
3. For x = - 20 , \( \left |- \dfrac{|x - 2|}{|-x + 9|} \right | = \dfrac{22}{29}\)
   
4. For x = - 3 , \( | - 3 x - x^2 | = 0 \)
   
5. For x = - 2 , \( x^{| x - 7|} = - 512\)

1. | a - b | = 0
   
2. | a - b | = a - b
   
3. | a - b | = b - a
4. \( \sqrt {3^2} = |3| = 3 \)
5. \( \sqrt {(- 3)^2} = |-3| = 3 \)
6. \( \sqrt { (12 - 20)^2 = 8} \)
7. \( | x^2 | = x^2\)
8. \( | (-x)^2 | = x^2\)
9. \( | (x + 1)^2 | = (x + 1)^2 \)
10. \( \sqrt{(x - y + z)^2} = |x - y + z|\)
11. \( \sqrt{sin^2(x)} = |sin(x)| \)

1. \( |x - 2| = 4 \) , two solutions: x = - 2 and x = 6
2. \( |x + 5| = 0 \) , one solution: x = - 5
3. \( |10 - x| = - 5 \) , no real solutions.

1. \( |x - 7| \gt 4 \) , solution set: x < 3 ? x > 11
2. \( |x + 5| \lt 9 \) , solution set: -14 < x < 4
3. \( |x + 8| \lt - 5 \) , solution set: {?}
4. \( |x + 8| \gt - 2 \) , solution set: {all real numbers}

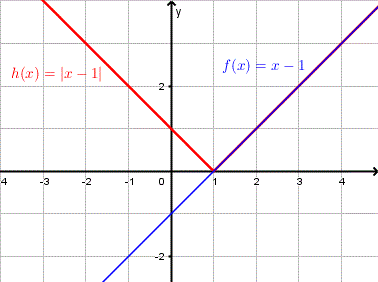
1. \( f(x) = x - 1 , h(x) = |f(x)| = |x - 1| \)
   For x - 1 ? 0 or x ? 1, h(x) = | x - 1 | = x - 1 and we therefore have h(x) = f(x) which we can be clearly seen from the graphs.
   For x - 1 < 0 or x < 1 , h(x) = |x - 1| = - (x - 1) = - f(x).
   Therefore for x < 1 h(x) = - f(x) which means that the graph of h is a reflection of the graph of f on the x axis and this is can be clearly seen on the graphs.
   
   
   
   
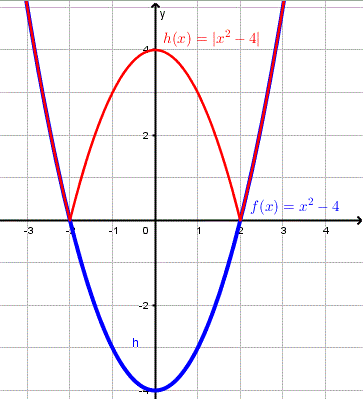
2. \( f(x) = x^2 - 4 , h(x) = |f(x)| = |x^2 - 4| \)
   For x² - 4 ? 0 or -2 ? x ? 2 , h(x) = |(x² - 4)| = - (x² - 4) = - f(x) . Therefore, on the interval -2 ? x ? 2, the graph of h is a reflection of the graph of f. Outside this interval, the two graphs coincide.
   
   
   
   
3. \( f(x) = \sin(x) , h(x) = |\sin(x)| \)
   Over intervals -2? to -? , 0 to ? , 2? to 3?, ... sin(x) ? 0 and h(x) = sin(x) = f(x) therefore the graphs of h and f coincide.
   For intervals - ? to 0 , ? to 2? ... sin(x) < 0 , h(x) = | sin(x) | = - sin(x) and the graph of h is a reflection of the graph of f on the x axis.
   
   
   

More References and Links