Find Reference Angle

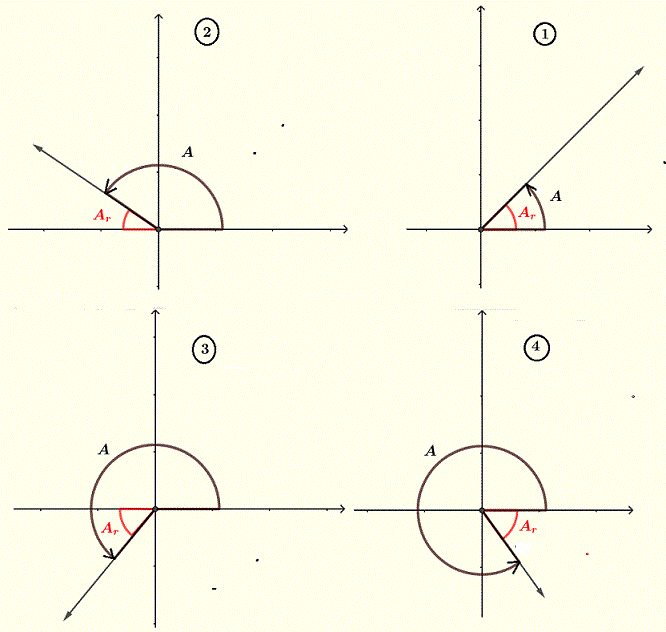
What is the reference angle to an angle in standard position? If A is an angle in standard position, its reference angle Ar is the acute angle formed by the x axis and the terminal side of angle A. See figure below.

reference angle

Two or more coterminal angles have the same reference angle.
Assume angle A is positive and less than 360° (2π), we have 4 possible cases:
1. If angle A is in quadrant I then the reference angle A r = A .
2. If angle A is in quadrant II then the reference angle A r = 180° - A if A is given degrees and A r = π - A if A is given in radians.
3. If angle A is in quadrant III then the reference angle A r = A - 180° if A is given degrees and A r = A - π if A is given in radians.
4. If angle A is in quadrant IV then the reference angle A r = 360° - A if A is given degrees and A r = 2π - A if A is given in radians.

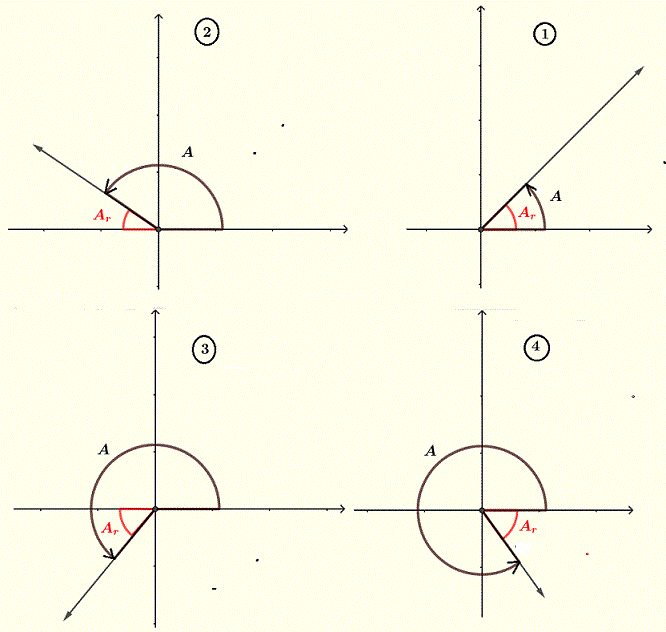
Example 1: Find the reference angle to angle A = 120 °.
Solution to example 1:
Angle A is in quadrant II and the reference angle is given by
A r = 180° - 120° = 60°

Example 2: Find the reference to angle A = - 15 π / 4.
Solution to example 2:
The given angle is not positive and less than 2π. We can use the positive and less than 2π coterminal Ac to angle A.
Ac = - 15 π / 4 + 2 (2 π) = π / 4
Angle A and Ac are coterminal and have the same reference angle. Ac is in quadrant I, therefore
A r = A c = π / 4

Example 3: Find the reference angle to angle A = - 30°
Solution to example 3:
Angle A is negative, in quadrant IV and its absolute value is less than 90°. Hence
A r = | -30° | = 30°

Exercises:Find the reference angle to angles
1. A = 1620°
2. A = - 29 π / 6
3. A = - π / 7
Solutions to Above Exercises:
1. A r = 25°
2. A r = π / 6
3. A r = π / 7


More references on angles.