An online calculator that completes the square of a quadratic expression.
Completing the square is to write a quadratic expression of the form $a x^2 + b x + c$ into the form $a (x + h)^2 + k $.
step 1: Factor coefficient $a$ out of the terms in $x$
$ax^2 + b x + c = a( x^2 + \dfrac{b}{a} x )+ c $
step 2: Add and subtract $ (b/2a)^2 $ inside the parentheses (it is like adding zero! and we therefore do no change the expression).
$ = a( x^2 + \dfrac{b}{a} x + (\dfrac{b}{2a})^2 - (\dfrac{b}{2a})^2 )+ c $
Group the first three terms inside the parentheses.
$ = a( x^2 + \dfrac{b}{a} x + (\dfrac{b}{2a})^2) - a (\dfrac{b}{2a})^2 + c $
The terms inside the parentheses are grouped as a square hence "completing the square".
$ = a( x + \dfrac{b}{2a})^2 - a (\dfrac{b}{2a})^2 + c $
The above may be written as
$ = a(x+h)^2 + k $
with $h = \dfrac{b}{2a}$ and $k = c - a (\dfrac{b}{2a})^2 $
Example 1: Complete the square in the expression $2x^2 + 6 x + 5/2$
Solution
Factor the coefficient of $x^2$ out of the terms in x.
$2x^2 + 6 x - 1 = 2(x^2 + 3) + 5/2$
add and subtract $(3/2)^2$ inside the parentheses
$ = 2(x^2 + 3 x + (3/2)^2 - (3/2)^2) + 5/2$
Group the first three terms inside the parentheses
$ = 2(x^2 + 3 x + (3/2)^2) - 2(3/2)^2 + 5/2$
Write the terms inside the parentheses as a square and group the constant terms outside the parentheses
$ = 2(x + 3/2)^2 - 2$
1 - Enter the coefficients a, b and c and press "Complete Square". a, b and c can be entered as integers, fractions or numbers with a decimal point as shown below. This calculator helps you practice on as many examples as you wish and check your answers.
The method of completing the square may be applied in the following situation
1) to solve quadratic equations.
Example solve: $2x^2 + 6 x + 5/2 = 0$
We have completed the square in example 1 for the expression $2x^2 + 6 x + 5/2 = 2(x + 3/2)^2 - 2$ and therefore solving the given equation is equivalent to solving the equation
$2(x + 3/2)^2 - 2 = 0$
$(x + 3/2)^2 = 1$
$ x + 3/2 = \pm \sqrt 1 $
$x = - 3/2 \pm 1 $ , 2 solutions : $x_1 = -5/2$ , $x_2 = - 1/2$
2) Find the vertex and x-intercepts of the graph of a quadratic function.
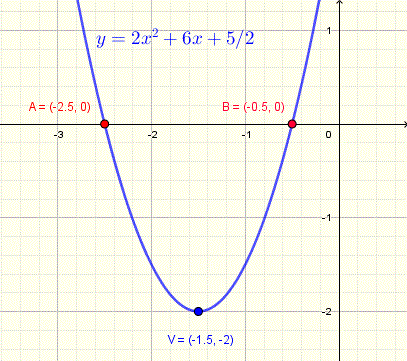
Example: Find the vertex and the x-intercepts of the graph of the function $ y = 2x^2 + 6 x + 5/2$
Use the equivalent expression obtained above
$ y = 2x^2 + 6 x + 5/2 = 2(x + 3/2)^2 - 2 = a(x + h) + k $
The vertex is at the point $(- h , k) = (- 3/2 , -2)$
The x-intercepts are the solutions of the equation $2x^2 + 6 x + 5/2 = 0$ which has been solved in example 1.
The graph below is that of the function $ y = 2x^2 + 6 x + 5/2$ with the x-intercepts and the vertex.
