Find the domain of a graph of a function; examples with solutions are presented. First the graphical meaning of the concept of the domain of a function is explained.
Find the domain of the graph of the function shown below and write it in both interval and inequality notations.
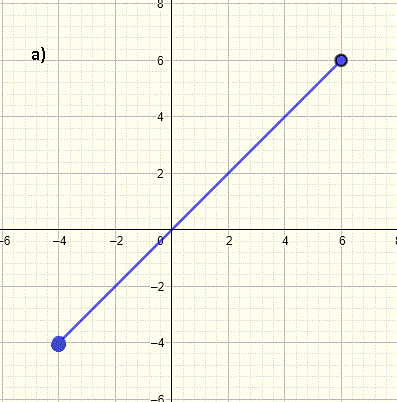
Solution to Example 1
The graph starts at \( x = -4 \) and ends \( x = 6 \). For all \( x \) between \( -4 \) and \( 6 \), there points on the graph. Hence the domain, in interval notation, is written as
\[ [-4 , 6] \]
In inequality notation, the domain is written as
\[ -4 \leq x \leq 6 \]
Note that we close the brackets of the interval because \( -4 \) and \( 6 \) are included in the domain which is indicated by the closed circles at \( x = -4 \) and \( x = 6 \).
What is the domain, in interval notation, of the graph of the function shown below?
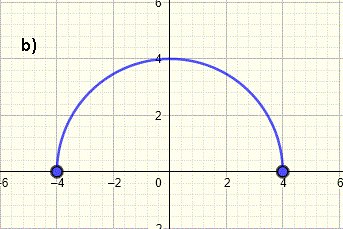
Solution to Example 2
The graph starts at \( x = -4 \) and ends \( x = 4 \). There are points on the graph for all values of \( x \) between \( -4 \) and \( 4 \) including at \( -4 \) and \( 4 \). Hence the domain, in interval notation, is written as
\[ [-4, 4] \]
What is the domain of the graph of the function?
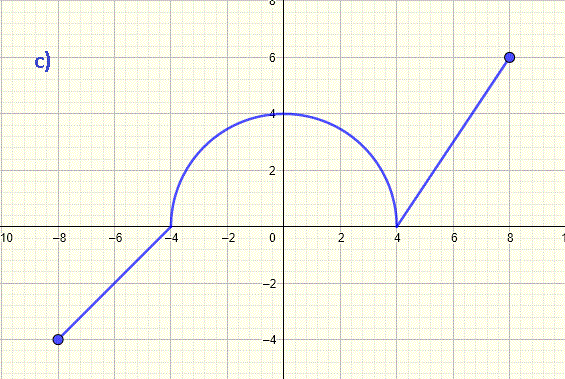
Solution to Example 3
The graph starts at \( x = -8 \) and ends \( x = 8 \). The graph is defined for all \( x \) between \( -8 \) and \( 8 \). We include \( -8 \) and \( 8 \) because of the closed circles at \( x = -8 \) and \( x = 8 \). Hence the domain, in interval notation, is written as
\[ [-8, 8] \]
Find the domain of the graph of the function shown below.
Solution to Example 4
The graph starts at \( x = -4 \) and ends \( x = 6 \). The graph is defined for all \( x \) between \( -4 \) and \( 6 \). The interval is closed at \( -4 \) and \( 6 \) because of the closed circles at \( x = -4 \) and \( x = 6 \). Hence the domain, in interval notation is written as
\[ [-4, 6] \]
Write the domain of the graph of the function shown below in interval and inequality notations.
Solution to Example 5
The graph starts at values of \( x > -4 \) and ends at values of \( x \lt 4 \). \( x = -4 \) and \( x = 4 \) are not included in the domain because of the open circles at these values. Hence the domain, in interval notation, is written as
\[ (-4 , 4) \]
Note that the interval is open to indicate that \( -4 \) and \( 4 \) are not included in the domain of the graph.
In inequality notation, the same domain is given by
\[ -4 \lt x \lt 4 \]
Note that the strict inequality sign (without equal) is used in the inequality notation of the domain because \( x = -4 \) and \( x = 4 \) are not included in the domain.
Write the domain of the graph of the function shown below in interval notation.
Solution to Example 6
The graph starts at values of \( x = -8 \) and ends at values of \( x \lt 2 \). The open circles at \( x = -4 \), \( x = -2 \), and \( x = 2 \) indicate that these values are not included in the domain. Hence the domain, in interval notation, is written as
\[ [-8, -4) \cup (-4, -2) \cup (-2, 2) \]
Note the interval is open at \( x = -4 \), \( x = -2 \), and \( x = 2 \) to indicate that these values are not included in the domain of the graph.
Write the domain of the graph of the function shown below in inequality notation.
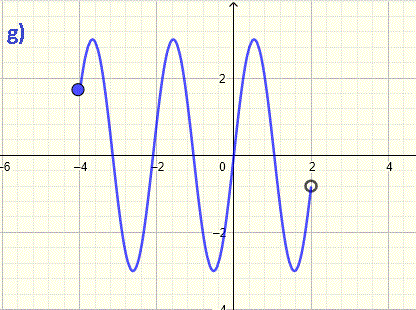
Solution to Example 7
The graph starts at \( x = -4 \) and ends \( x \lt 2 \). The domain does not include \( x = 2 \) because of the open circle at \( x = 2 \). Hence the domain, in inequality notation, is written as
\[ -4 \leq x \lt 2 \]
Write the domain of the graph of the function shown below using interval notation
Solution to Example 8
The graph is made up of three parts. The left part is defined for all values of \( x \) between \( -4 \) and \( -2 \). The part in the center is defined on the interval \( x > 0 \) and \( x \leq 4 \). The part on the right is defined for \( x > 6 \) and \( x \leq 8 \). The domain is written as a union of three intervals as follows
\[ [-4, -2] \cup (0, 4] \cup (6, 8] \]
