Definition and Equation of an Ellipse with Vertical Axis
An ellipse is the set of all points \( M(x,y)\) in a plane such that the sum of the distances from \( M \) to fixed points \( F_1 \) and \( F_2 \) called the foci (plurial of focus) is equal to a constant.
\( \overline{MF_1} + \overline{MF_2} = \sqrt{(x+c)^2+y^2} + \sqrt{(x-c)^2+y^2} = 2 a \)
For \( a \ge b \ge 0 \), eliminating the square roots by squaring and simplifying using the relationship \( a^2 = b^2 + c^2\), we can end up with the standard equation of an ellispe given by:
\( \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \)
The width of the ellipse is \( 2 a \) and the height is \( 2 b \)
Point \(O(0,0)\) is the center of the ellipse.
Points \( V_1(a,0) \) and \( V_2(-a,0) \) are called the vertices of the ellipse.
The foci are at \( F_1(c,0) \) and \( F_2(-c,0) \)
Example 1
An ellipse centered at \( (0,0) \) has x intercepts at \( (7,0) \) and \( ( -7 ,0) \) and y intercepts at \( (0,4) \) and \( ( 0,-4) \). Find the equation of the ellipse and the foci \( F_1 \) and \( F_2 \)
Solution to Example 1
The equation of an ellipse whose center is at the origin is given by
\( \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \) , \( a \gt 0 \) and \( b \gt 0 \)
Find the x axis by setting y = 0 in the above equation
\( \dfrac{x^2}{a^2} + \dfrac{0^2}{b^2} = 1 \)
Simplify
\( \dfrac{x^2}{a^2} = 1 \)
Solve for \( x \)
\( x = a \) and \( x = - a \)
The x intercepts are given by \( (7,0) \) and \( ( -7 ,0) \) which gives \( a = 7 \).
Find the y axis by setting x = 0 in the general given above equation
\( \dfrac{0^2}{a^2} + \dfrac{y^2}{b^2} = 1 \)
Simplify
\( \dfrac{y^2}{b^2} = 1 \)
Solve for \( y \)
\( y = b \) and \( y = - b \)
The y intercepts are given by \( (0,4) \) and \( ( 0 , -4) \) which gives \( b = 4 \).
In order to find the foci, we first need to find parameter \( c \) which is related to \( a \) and \( b \) by
\( a^2 = b^2 + c^2\)
Substitute \( a \) and \( b \) by their values and solve for \(c \)
\( 7^2 = 4^2 + c^2\)
\( c = \sqrt{49 - 16} = \sqrt{33} \)
The coordinates of the two foci F1 and F2 are given by
\( F_1(c,0) = F_1(\sqrt{33} , 0) \) and \( F_1( - c,0) = F_1( - \sqrt{33} , 0) \)
General Equation of an Ellipse
We can generalize and write the equation of an ellipse whose center is at \( O(h,k) \) as follows
with foci at \( F_1(c+h,k) \) and \( F_2(-c+h,k) \) and vertices at \( V_1(a+h,k) \) and \( V_2(-a+h,k) \).
Example 2
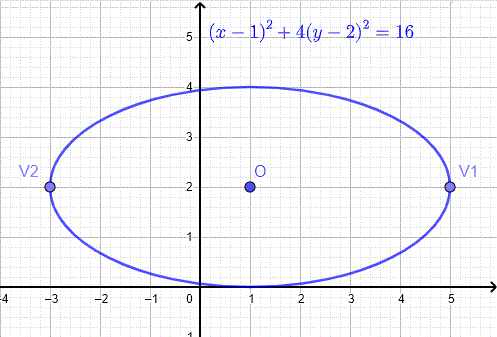
Find the center, foci and vertices of the ellipse given by the equation \( (x - 1)^2 + 4(y-2)^2 = 16 \) then use a graphing calculator to graph the given equation and check your answers.
Solution to Example 2
Rewrite the given equation in standard form by dividing all terms by 16.
\( \dfrac{(x - 1)^2}{16} + \dfrac{4(y-2)^2}{16} = \dfrac{16}{16} \) .
Simplify and write the denominators of the terms on the left as squares
\( \dfrac{(x - 1)^2}{4^2} + \dfrac{(y-2)^2}{2^2} = 1 \)
Compare the above equation of an ellipse in standard for to the general equation \( \dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1 \) and identify the parameters \( a, b, h\) and \( k \).
\(a = 4, b = 2, h = 1\) and \( k = 2 \)
The center is at the point \( O(h,k) = O(1,2) \)
Find the parameter \( c \) using the relationship \( a^2 = b^2 + c^2\)
\(c = \sqrt{a^2 - b^2} = \sqrt{16 - 4} = 2 \sqrt{3} \)
The foci are at the points
\( F_1(c+h,k) = F_1(2 \sqrt{3}+1,2) \) and \( F_2(-c+h,k) = F_2(-2 \sqrt{3}+1,2) \)
The vertices are at the points
\( V_1(a+h,k) = V_1(5,2) \) and \( V_2(-a+h,k) = V_2(-3,2) \)
The graph of the given equation \( (x - 1)^2 + 4(y-2)^2 = 16 \) is shown below and it is that of an ellipse with center at \(O(1,2)\) and vertices at \(V_1(5,2) \) and \(V_2(-3,2) \) as calculated above.
Interactive Turorial on Equation of an Ellipse
An app to explore the equation of a parabola and its properties is now presented. The equation used is the standard equation that has the form
The exploration is carried out by changing the parameters \( a, b, h \) and \( k \) included in the above equation. The default values, when you open this page, are: \( a = 4, b = 2, h = 2 \) and \( k = 3 \).
Some activities are listed below but many other activities may be generated.
Click on the button "Plot Equation" to start.
Hover the mousse cursor on the graph or plotted point to read the coordinates.
Click the button above "Plot Equation". You may hover the mousse cursor over the graph of the ellipse and the points to read the coordinates. You may also Hover the mousse cursor on the top right of the graph to have the options of zooming, downloading the graph as a png file, ...
1 - Select a point M on the graph of the ellipse, hover the mousse over it and read the coordinates. Read the coordinates of F1 and F2 (right legend) or hover the mousse and read the coordinates and show that the sum of the distances \( \overline{MF_1} + \overline{MF_2} \) is close to \( 2a\).
You may do the above activity for different values of \( a, b, h\) and \( k \) and as many points as needed to better understand the definition of an ellipse.
2 - Use the values of \( a \) and \( b \) to find \( c \) using the relationship between \( a, b\) and \( c \) given by \( a^2 = b^2 + c^2\).
Use the above results to find the coordinates of \( F_1, F_2, V_1 \) and \( V_2 \) and check the results graphically.
3 - Set \( a, b, h\) and \( k \) to some values. Find the x and y intercepts and check your results graphically.
4 - Exercise:
Show by algebraic calculations that the following equation \( \dfrac{(x + 2)^2}{5} + 5(y-3)^2 = 5 \) is that of an ellipse and find the center, foci and vertices of the ellipse given by the equation then use the app to graph it and check your answers.
