Equation of Ellipse - Problems

This is a tutorial with detailed solutions to problems related to the ellipse equation. An HTML5 Applet to Explore Equations of Ellipses is also included in this website.

Review

An ellipse with center at the origin \( (0,0) \), is the graph of

with \(a > b > 0\).

The length of the major axis is \(2a\), and the length of the minor axis is \(2b\). The two foci (foci is the plural of focus) are at \((\pm c , 0)\) or at \((0 , \pm c)\), where \(c^2 = a^2 - b^2\).

Problem 1

Given the following equation

\(9x^2 + 4y^2 = 36\)

a) Find the \(x\) and \(y\) intercepts of the graph of the equation.

b) Find the coordinates of the foci.

c) Find the length of the major and minor axes.

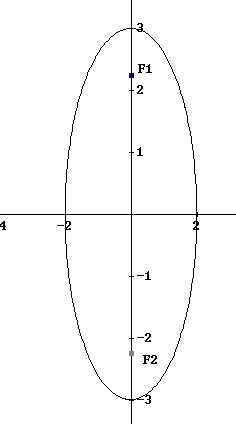
d) Sketch the graph of the equation.

a) We first write the given equation in standard form by dividing both sides of the equation by 36 and simplify

\(\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\)

We now identify the equation obtained with one of the standard equations in the review above and we can say that the given equation is that of an ellipse with \(a = 3\) and \(b = 2\). NOTE: \(a > b\)

Set \(y = 0\) in the equation obtained and find the \(x\) intercepts.

\(\dfrac{x^2}{2^2} = 1\)

Solve for \(x\).

\(x^2 = 2^2\)

\(x = \pm 2\)

Set \(x = 0\) in the equation obtained and find the \(y\) intercepts.

\(\dfrac{y^2}{3^2} = 1\)

Solve for \(y\).

\(y^2 = 3^2\)

\(y = \pm 3\)

b) We need to find \(c\) first.

\(c^2 = a^2 - b^2\)

a and b were found in part a)

\(c^2 = 3^2 - 2^2\)

\(c^2 = 5\)

Solve for \(c\) to obtain

\(c = \pm \sqrt{5}\)

The foci are \(F_1(0 , \sqrt{5})\) and \(F_2(0 , - \sqrt{5})\)

c) The major axis length is given by \(2a = 6\)

The minor axis length is given by \(2b = 4\)

d) Locate the \(x\) and \(y\) intercepts, find extra points if needed and sketch.

Matched Problem: Given the following equation

\(4x^2 + 9y^2 = 36\)

a) Find the \(x\) and \(y\) intercepts of the graph of the equation.

b) Find the coordinates of the foci.

c) Find the length of the major and minor axes.

d) Sketch the graph of the equation.

More Links and References on Ellipses