
This tutorial presents questions on solving quadratic equations using the discriminant and quadratic formula with detailed step-by-step solutions. We explain how the sign of the discriminant affects the number and type of solutions. Additional questions and solutions are provided at the bottom of this page.
More quadratic equation questions and solutions, as well as a Step by Step Quadratic Equation Solver, are included.
A quadratic equation in one variable has the form:
\[ ax^2 + bx + c = 0 \] where \(a \neq 0\) and \(a, b, c\) are constants.
The solutions are given by the quadratic formula:
\[ x_1 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}, \quad x_2 = \frac{-b - \sqrt{b^2 - 4ac}}{2a} \]
The discriminant is the quantity:
\[ \Delta = b^2 - 4ac \]
The discriminant determines the number and nature of solutions:
Solve the quadratic equation:
\[ x^2 + 3x = 4 \]Rewrite with zero on the right-hand side:
\[ x^2 + 3x - 4 = 0 \]Discriminant:
\[ \Delta = b^2 - 4ac = 3^2 - 4(1)(-4) = 25 \]Since \(\Delta > 0\), two real solutions exist:
\[ x_1 = \frac{-3 + \sqrt{25}}{2} = 1, \quad x_2 = \frac{-3 - \sqrt{25}}{2} = -4 \]Check:
\[ x = 1 \Rightarrow 1^2 + 3(1) = 4, \quad x = -4 \Rightarrow (-4)^2 + 3(-4) = 4 \]Conclusion: Solutions: \(x = 1, -4\)
Solve:
\[ \frac{x^2}{3} + 3 = 2x \]Multiply through by 3:
\[ x^2 + 9 = 6x \quad \Rightarrow \quad x^2 - 6x + 9 = 0 \]Discriminant:
\[ \Delta = (-6)^2 - 4(1)(9) = 0 \]Single solution:
\[ x = \frac{-b}{2a} = \frac{6}{2} = 3 \]Check: \(\frac{3^2}{3} + 3 = 6 = 2 \cdot 3\)
Conclusion: One real solution: \(x = 3\)
Solve:
\[ x^2 - 4x + 13 = 0 \]Discriminant:
\[ \Delta = (-4)^2 - 4(1)(13) = -36 \]Since \(\Delta < 0\), solutions are complex:
\[ x_1 = \frac{4 + 6i}{2} = 2 + 3i, \quad x_2 = \frac{4 - 6i}{2} = 2 - 3i \]Conclusion: Two complex conjugate solutions: \(x = 2 + 3i, 2 - 3i\)
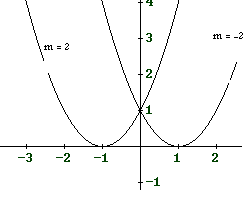
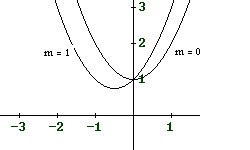
Solve for \(m\) in:
\[ x^2 + mx + 1 = 0 \]


