3D Shapes Volume Problems

Problems on 3D shapes, such as prisms, cube, cylinder, volume are presented along with detailed solutions

Problem 1

A rectangular prism of volume 3200 mm3 has a rectangular base of length 10 mm and width 8 mm. Find the height h of the prism.
rectangular prism problem 1

Solution to Problem 1:
  • Volume is given by by
    volume = length * width * height = 10 mm * 8 mm * h = 3200 mm3
  • Solve for h
    h = 3200 mm3 / 80 mm2 = 40 mm

Problem 2

The area of one square face of a cube is equal to 64 cm2. Find the volume of the cube.
cube problem 2

Solution to Problem 2:

  • The area of one square face is given by
    s * s = 64 cm2
  • Solve for s
    s = SQRT(64 cm2) = 8 cm
  • The volume V of the given cube is given by
    V = s3 = 83 = 512 cm3

Problem 3

The triangular base of a prism is a right triangle of sides a and b = 2a. The height h of the prism is equal to 10 mm and its volume is equal to 40 mm3, find the lengths of the sides a and b of the triangle.
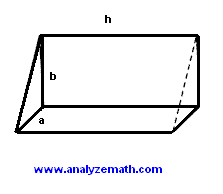
triangular prism problem 3

Solution to Problem 3:

  • The volume V of the prism is given by
    V = (1/2) a * b * h = 40 mm3
  • Substitute b by 2a and h by its value
    40 mm3 = a2 * 10 mm
  • Solve for a and calculate b
    a = 2 mm
    b = 2a = 4 mm

Problem 4

Find the volume of the given L-shaped rectangular structure.
L-shaped structure problem 4

Solution to Problem 4:

  • We can think of the given shape as a larger rectangular prism of dimensions 60, 80 and 10 mm from which a smaller prism of dimensions 40, 60 and 10 mm has been cut. Hence the volume V of the given 3D shape
    V = 60 * 80 * 10 mm3 - 40 * 60 * 10 mm3 = 24000 mm3

Problem 5

Find the thickness x of the hollow cylinder of height 100 cm if the volume between the inner and outer cylinders is equal to 11000 Pi mm3 and the outer diameter is 12 mm.
Hollow cylinder 5

Solution to Problem 5:

  • If R and r are the outer and inner radii of the hollow cylinder the volume V between the inner and outer cylinders is given by
    V = h*(Pi R2 - Pi r2) = 11000 Pi
  • Also R = 6 and h = 100 cm = 1000 mm, hence
    1000 * (36 Pi - Pi r2) = 11000 Pi
  • Solve for r
    r = 5 mm
  • Find x
    x = R - r = 1 mm

Problem 6

Find x so that the volume of the U-shaped rectangular structure is equal to 165 cm3.
U-shaped structure problem 6

Solution to Problem 6:

  • We can think of the given shape as a larger rectangular prism of dimensons 8, 3 and 10 cm from which a smaller prism of dimensions x, x and 3 cm has been cut. Hence the volume V of the given 3D shape is given by
    V = 8 * 3 * 10 mm3 - x * x * 3 mm3 = 165 cm3
  • Solve for x
    x = 5 cm

Problem 7

Find the volume of the hexagonal prism whose base is a regular hexagon of side x = 10 cm.
hexagonal prism 7

Solution to Problem 7:

  • The hexagon is made up of 6 equilateral triangles, hence the area A of the base
    A = 6 (x2 SQRT(3) / 4)
  • Hence the volume V of the prism
    V = 24 * 6 (102 SQRT(3) / 4) cm 2 = 6235.4 cm3 (rounded to 1 decimal place)

More References and Links to Triangles and Geometry

Geometry Tutorials, Problems and Interactive Applets.