Kite Within a Square - Problem With Solution
A problem on finding the sine of the angle of a kite within a square is presented along with detailed solution.
Problem
In the figure below, ABCD is a square whose side has a length equal to 2 units. Points M and N are on the sides BC and CD such that x is the length of BM and DN. Express sin(a) as a function of x.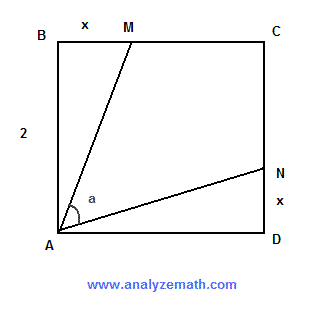
Solution to Problem :
-
The right triangles ABM and ADN are congruent. The area of one of them is given by
(1/2)(2)(x) = x
-
We now subtract the areas of the two right triangles ABM and ADN from the area of the square to obtain the area of the kite AMCN.
area of AMCN = (2)(2) - 2 x = 4 - 2x
-
The area of the kite AMCN can also be found as the area of the isosceles triangle AMN plus the right triangle MCN
area of isosceles triangle AMN = (1/2) sin(a) (AM)(AN) = (1/2) sin(a) AM2 = (1/2) sin(a) (x2 + 4)
area of MCN = (1/2)(x - 2)2
area of AMCN = (1/2) sin(a) (x2 + 4) + (1/2)(x - 2)2
-
We now equate the two expressions for the area of the kite AMCN found above to obtain
(1/2) sin(a) (x2 + 4) + (1/2)(x - 2)2 = 4 - 2x
-
Multiply all terms of the above equation by 2 to obtain
sin(a) (x2 + 4) + (x - 2)2 = 2(4 - 2x)
-
Solve for sin(a) to obtain.
sin(a) = (4 - x2) / (4 + x2)
-
As an exercise, put x = 0 in the expression of sin(a) obtained and find angle a. Check your answer using the geometrical figure shown above. Set x = 0 and check your answer. Any contradiction in your answers?
More References and links to Geometry ProblemsGeometry Tutorials, Problems and Interactive Applets.
|
