Three Tangent Circles - Problem With Solution

A problem, on three tangent circles, is presented along with detailed solution.

Problem

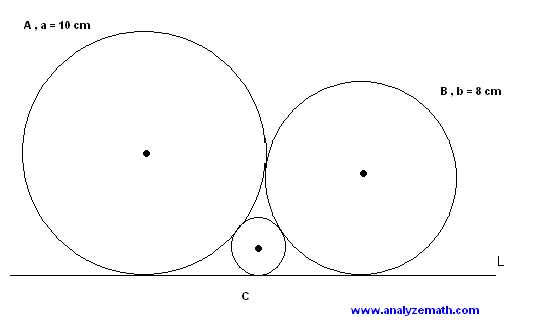
In the figure below, three circles are tangent to each other and to line L. The radius of circle A is equal to 10 cm and the radius of circle B is equal to 8 cm. Find the radius of circle C.
three tangent circles problem
Solution to Problem

  • Let a, b and c be the radii of the three circles. We first draw the lines AA', BB' and CC' perpendicular to line L. B'C, CA' and BA" are parallel to line L.
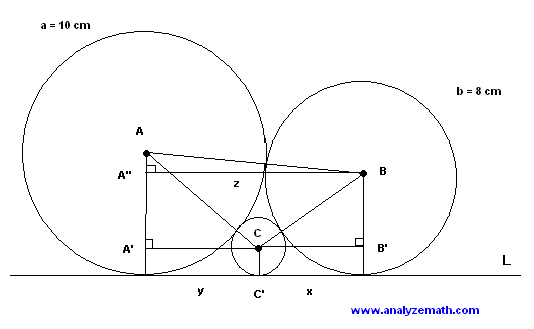
    three tangent circles solution

  • Let x = B'C, y=A'C and z = BA". Pythagora's theorem applied to the right triangle BCB' gives
    x 2 + BB' 2 = BC 2
  • Note that BB' = b - c and BC = b + c. The above equation may be written as follows
    x 2 + (b - c) 2 = (b + c) 2
  • Expand the above, group like terms and solve for x
    x 2 = 4 b c
    x = 2 Square Root( b c )
  • Use Pythagora's theorem to triangle AA'C to obtain
    y 2 + (a - c) 2 = (a + c) 2
  • Expand, group like terms and solve for y
    y 2 = 4 a c
    y = 2 Square Root( a c )
  • Use Pythagora's theorem to triangle AA"B to obtain
    z 2 + (a - b) 2 = (a + b) 2
  • Expand, group and solve for z
    z 2 = 4 a b
    z = 2 Square Root( a b )
  • We now use the fact that z = x + y to write
    Square Root( a b ) = Square Root( b c )+ Square Root( a c )
  • Solve the above for c
    Square Root( a b ) = Square Root( c )Square Root ( b )+ Square Root( c )Square Root( a )
    Square Root( c ) = Square Root( a b ) / [ Square Root ( b )+ Square Root( a ) ]
    c = ( a b ) / [ Square Root ( b )+ Square Root( a ) ] 2
  • Substitute a and b by their values to obtain c
    c = 10 * 8 / [ Square Root ( 8 )+ Square Root( 10 ) ] 2
    c = 2.2 cm (rounded to 1 decimal place)

More References and Links to Geometry Problems

Geometry Tutorials, Problems and Interactive Applets.