Solve Triangle Given Its Perimeter, Altitute and Angle - Problem With Solution

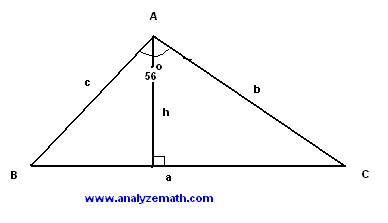
Solution to Problem :

• The given perimeter p = 100 gives an equation as follows
  
  a + b + c = p      (equation 1)
  
  
• The area of the triangle may be calculated using sides c and b as follows
  
  area = (1 / 2) b c sin (A)
  
  
• But the area of the triangle may also be calculated using the altitude h and corresponding base a as follows
  
  area = (1 / 2) h a
  
  
• We now combine the two expressions for the area to obtain an equation as follows
  
  b c sin (A) = h a      (equation 2)
  
  
• A third equation is obtained using the law of cosine as follows
  
  a ² = b ² + c ² - 2 b c cos (A)      (equation 3)
  
  
• We now have 3 equations with 3 unknowns which we have to solve. Equation (1) gives
  
  a = p - (b + c)
  
  
• Substitute the above into equation (3) to obtain
  
  (p - (b + c)) ² = b ² + c ² - 2 b c cos (A)
  
  
• Expand the left hand side of the above equation and simplify
  
  p ² + (b + c)) ² - 2 p (b + c) = b ² + c ² - 2 b c cos (A)
  
  p ² + b ² + c ² + 2 b c - 2 p (b + c) = b ² + c ² - 2 b c cos (A)
  
  p ² + 2 b c - 2 p (b + c) = - 2 b c cos (A)      (equation 4)
  
  
• We now use a = p - (b + c) in equation (2) and write
  
  b c sin (A) = h (p - (b + c))
  
  
• which may be written as follows
  
  b c sin (A) = h p - h (b + c)      (equation 5)
  
  
• We now define two variables as follows.
  
  Z = b + c and Y = b c
  
  
• and rewrite equations 4 and 5 as follows.
  
  p ² + 2 Y - 2 p Z = - 2 Y cos (A)
  
  Y sin (A) = h p - h Z
  
  
• The above equations make a system of linear equations with unknowns Z and Y.
  
  - 2 p Z + 2 (1 + cos (A)) Y = - p ²
  
  h Z + sin (A) Y = h p
  
  
• We now substitute p, h and angle A by their values.
  
  - 200 Z + Y (2 + 2 cos (56)) = - 10000
  
  18 Z + Y sin (56) = 1800
  
  
• Solve the above system to obtain
  
  Z = 62.6456 and Y = 811.035
  
  
• We now substitute Z by b + c and Y by b c to obtain two equations in b and c as follows.
  
  b + c = 62.6456 and b c = 811.035
  
  
• We now combine the above equations to obtain an equation in one unknown as follows.
  
  b + 811.035 / b = 62.6456
  
  
• Multiply all terms to obtain a quadratic equation.
  
  b ² + 811.035 = 62.6456 b
  
  
• Solve to obtain.
  
  b = 44.3643 and b = 18.2812
  
  
• We now use the equation b c = 811.035 to find c.
  
  for b = 44.3643 , c = 18.2812
  
  and for b = 18.2812, c = 44.3643
  
  
• It is in fact one solution since c and b are interchangeable. let the solution be b = 44.3643 units and c = 18.2812 units and find the third side using equation (3)
  
  a ² = b ² + c ² - 2 b c cos (A)
  
  a = sqrt [ 44.3643 ² + 18.2812 ² - 2*44.3643*18.2812 cos (56) ]
  
  a = 37.3543 units
• As an example check that the perimeter of the triangle is equal to 100 units.

More references to geometry problems.